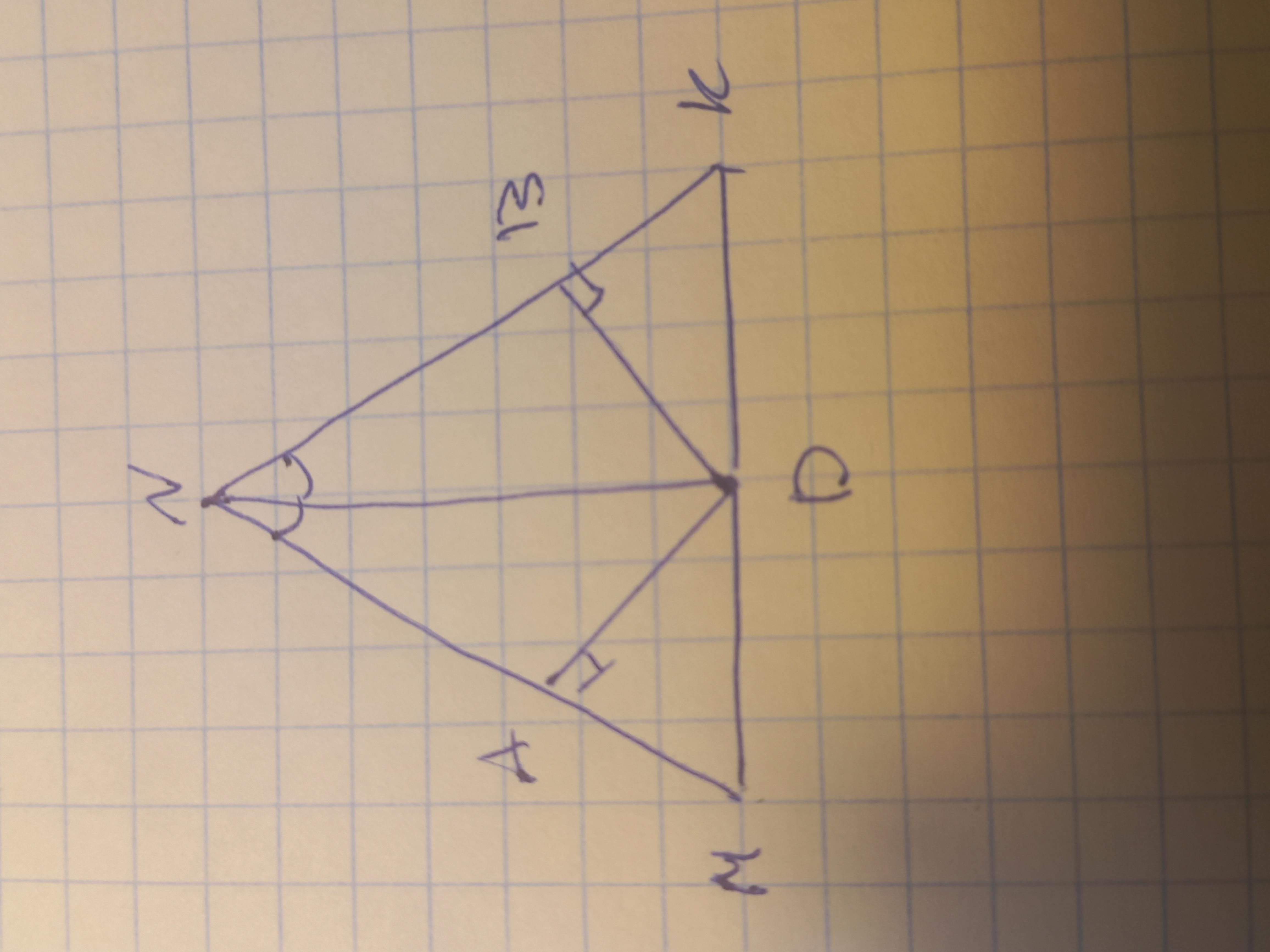
В равнобедренном треугольнике MNK точка D - СЕРЕДИНА ОСНОВАНИЯ MK, DA и DB перпендикулярны к боковым сторонам.
Докажите что DA = DB
Ответы
Ответ дал:
1
Ответ:
Объяснение:
Проведем медиану ND к основанию. Поскольку МNK равнобедренный, то ND биссектриса. В таком случае углы AND и BND равны. Поскольку АD и BD перпендикулярны боковым сторонам, то треугольники ADN и BDN прямоугольные. А дальше чисто равенство:
1. Углы AND и BND равны, тк ND биссектриса
2. ND - общая сторона и гипотенуза для обоих треугольников
Вывод: прямоугольные треугольники равны по гипотенузе и углу и AD = BD как соответственные элементы в равных треугольниках
Приложения:
pirimovairma69:
Спасибо большое
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
9 лет назад