Ответы
Ответ дал:
1
ответ 2
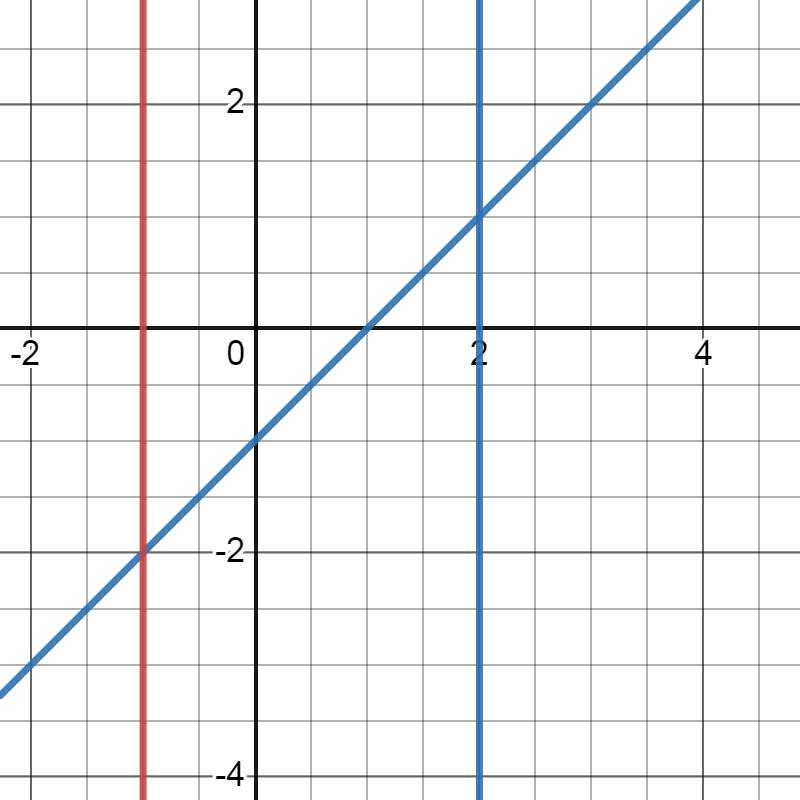
данная фигура представляет собой два прямогольных треугольника .
у(2)=2-1=1 площадь первого треугольника 2*1/2=1
у(-1)=-2
площадь второго 2*1/2=1
площадь фтгуры равна 1+1=2
данная фигура представляет собой два прямогольных треугольника .
у(2)=2-1=1 площадь первого треугольника 2*1/2=1
у(-1)=-2
площадь второго 2*1/2=1
площадь фтгуры равна 1+1=2
Ответ дал:
0
Объяснение:
Ответ: S=2,5 кв. ед.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад