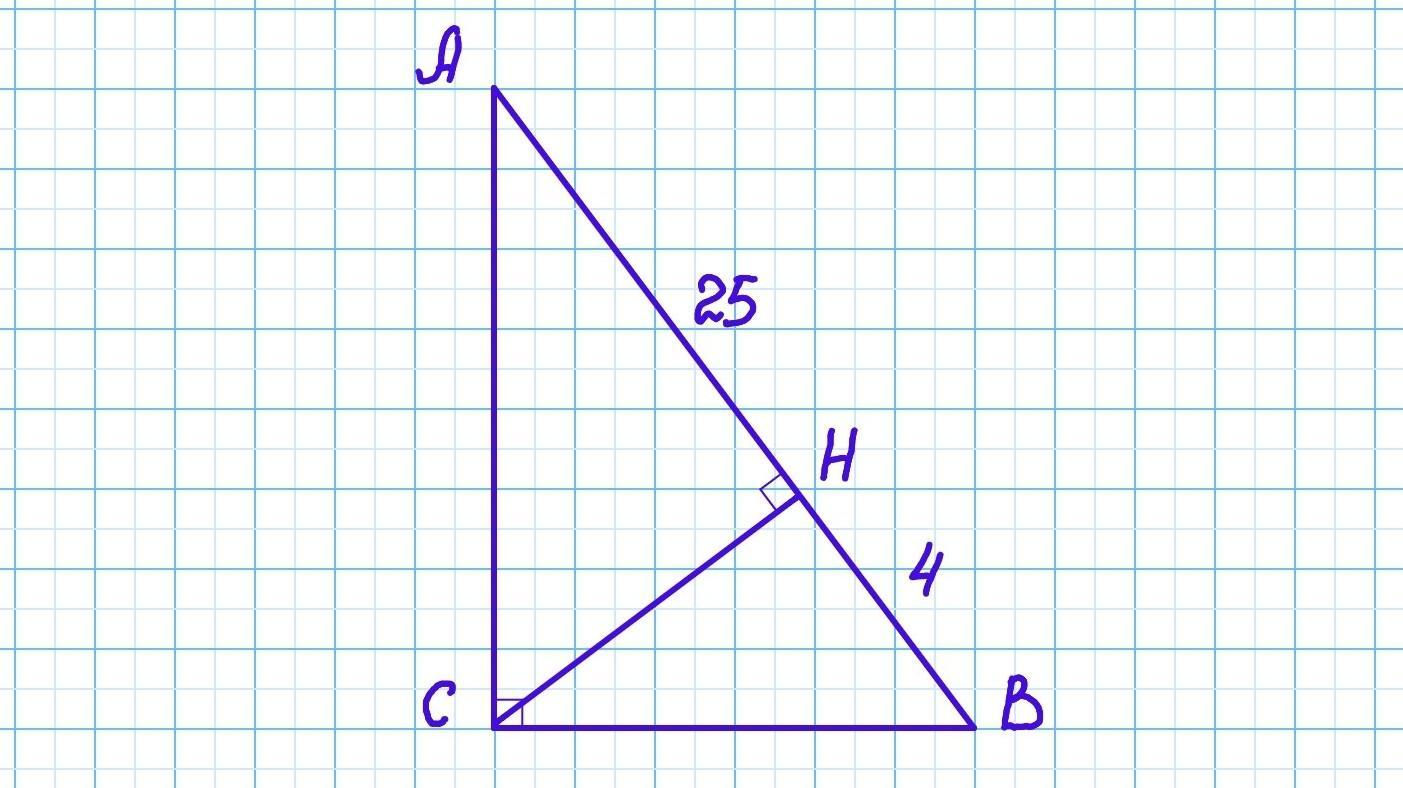
В прямокутному трикутнику висота проведена з прямого кута ділить гіпотенузу на відрізки 4 і 25см. Знайти сторони трикутника. Висоту трикутника. Кути трикутника. Радіус і вписаного кола навколо трикутника. Площа трикутника

Ответы

Ответ дал: ReMiDa

Ответ:

1) АВ=29см, АС=5√29 см, ВС= 2√29 см.

2) Висота СН=10см.

3)∠А ≈ 21,8°, ∠B ≈ 68,2°

4)R=14,5см, $r\approx 4,35$ см

5)S=145см²

Объяснение:

В прямокутному трикутнику висота проведена з прямого кута ділить гіпотенузу на відрізки 4 і 25см. Знайти сторони трикутника. Висоту трикутника. Кути трикутника. Радіус і вписаного кола навколо трикутника. Площу трикутника.

1) Знайдемо сторони трикутника

Гіпотенузу знаходимо через суму відрізків: АВ=АН+НВ=25+4= 29 см

Квадрат катета прямокутного трикутника дорівнює добутку гіпотенузи і проекції цього катета на гіпотенузу.

АС²=АВ•АН=29•25, АС=5√29 см

ВС²=АВ•НВ=29•4, ВС= 2√29 см

2) Знайдемо висоту трикутника

Квадрат висоти прямокутного трикутника, проведеної до гіпотенузи, дорівнює добутку проекцій катетів на гіпотенузу.

СН²=АН•НВ=25•4=100, СН=√100=10см.

3) Знайдемо кути трикутника.

Тангенсом гострого кута прямокутного трикутника називають відношення протилежного катета до прилеглого.

$tq \angle A = \dfrac{BC}{AC} = \dfrac{2 \sqrt{29} }{5 \sqrt{29} } = \dfrac{2}{5}$

∠А=arctg 2/5=arctg 0,4 ≈ 21,8°

$tq \angle B = \dfrac{AC}{BC} = \dfrac{5 \sqrt{29} }{2 \sqrt{29} } = \dfrac{5}{2}$

∠B=arctg 5/2=arctg 2,5 ≈ 68,2°.

Або, так як сума гострих кутів прямокутного трикутника дорівнює 90°, ∠В=90°-21,8=68,2°.

4)Знайдемо радіус описаного та вписаного кола.

У прямокутному трикутнику радіус описаного кола дорівнює половині гіпотенузи R = c / 2, а радіус вписаного кола дорівнює половині різниці суми катетів і гіпотенузи r = (a + b – c) / 2, де a і b — катети прямокутного трикутника, а c — його гіпотенуза.

R=AB/2=29/2=14,5 см

$r = \dfrac{AC + BC - AB}{2} = \dfrac{5 \sqrt{29} + 2 \sqrt{29} - 29 }{2} = \dfrac{7 \sqrt{29} - 29}{2}\approx 4.35$ см