100 БАЛЛОВ СРОЧНО
Дано дифференциальное уравнение второго порядка, которое
допускает понижение порядка.
Приложения:
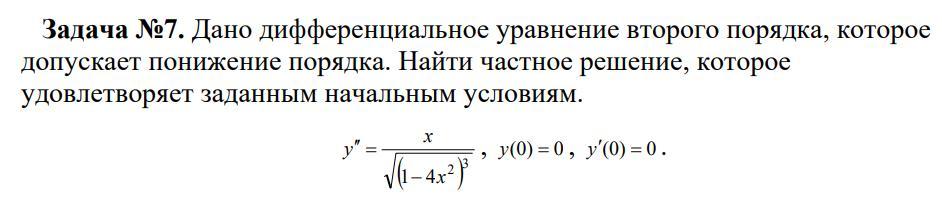
Ответы
Ответ дал:
0
Ответ:
Задача Коши для д.у. 2 порядка.
Частное решение: .
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад