Question

Помогите пожалуйста решить (подробно нужно) ​

Answer 1

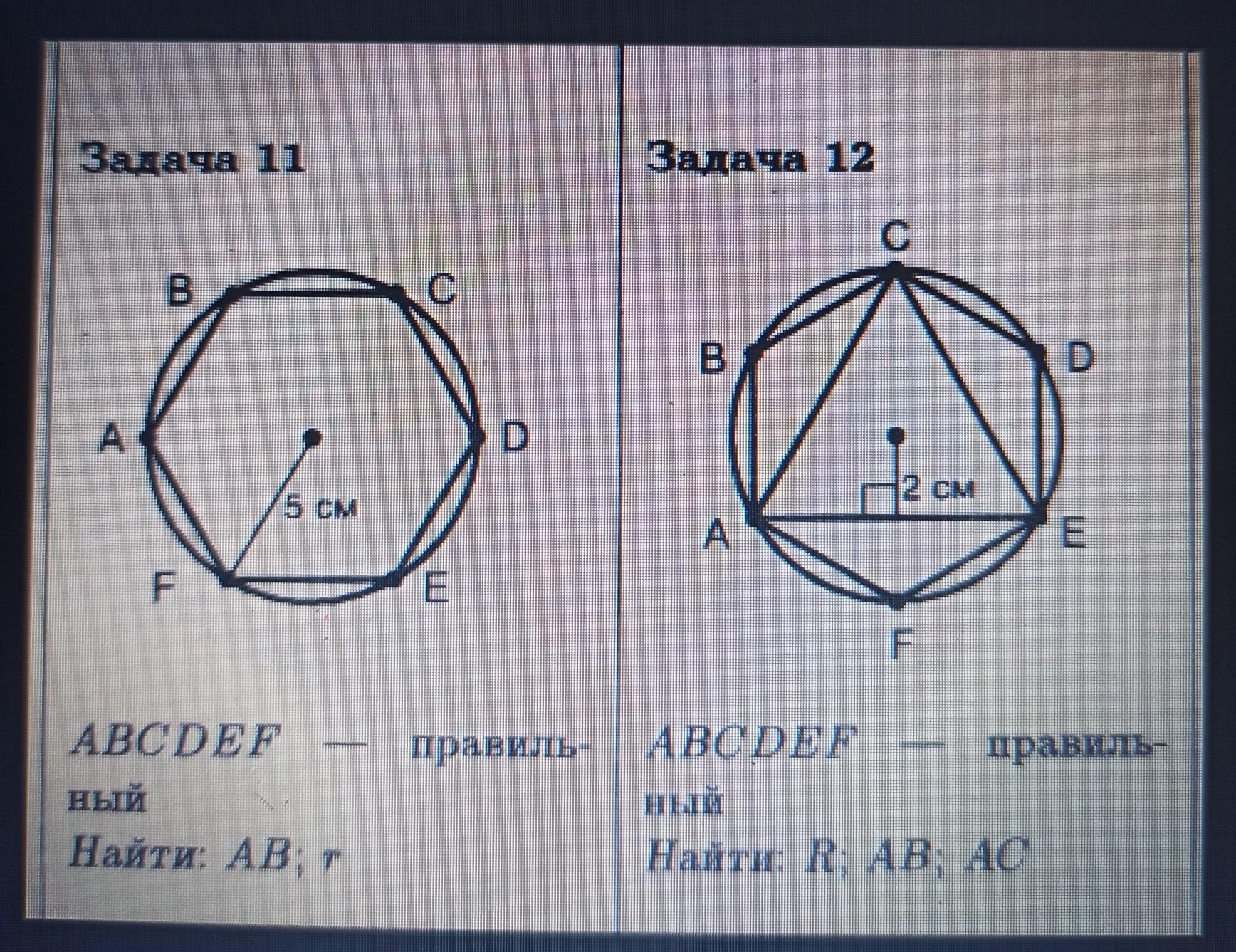
Задача 11

Радиус окружности описанной около правильного шестиугольника равен стороне шестиугольника .

$\displaystyle\bf\\AB=R=5 \ cm$

Радиус окружности вписанной в правильный шестиугольник можно найти по формуле :

$\displaystyle\bf\\r=\frac{AB\cdot \sqrt{3} }{2} =\frac{5\sqrt{3} }{2}$

Задача 12

Радиус окружности вписанной в правильный треугольник равен :

r₃ = 2 см , значит сторону правильного треугольника можно найти по формуле :

$\displaystyle\bf\\AC=2\sqrt{3} \cdot r=2\sqrt{3} \cdot 2=4\sqrt{3} \ cm$

Радиус окружности описанной около правильного треугольника можно найти по формуле :

$\displaystyle\bf\\R=\frac{AC}{\sqrt{3} } =\frac{4\sqrt{3} }{\sqrt{3} }=4 \ cm$

Эта же окружность описана около правильного шестиугольника , значит его сторона равна радиусу этой окружности :

$\displaystyle\bf\\AB=R=4 \ cm$