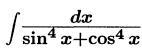Question

Решить интеграл ⠀⠀⠀⠀

Answer 1

Ответ:

$\int\limits {\dfrac{dx}{sin^{4}x+cos^{4} x } } =\dfrac{1}{\sqrt{2} } \cdot arctg \dfrac{tg2x}{\sqrt{2} } +C$

Пошаговое объяснение:

Вычислить неопределенный интеграл

$\int\limits {\dfrac{dx}{sin^{4}x+cos^{4} x } }$

Преобразуем знаменатель

$sin^{4} x+cos ^{4} x=(sin^{2} x)^{2} +(cos^{2} x)^{2} +2sin^{2} x\cdot cos^{2} x-2sin^{2} x\cdot cos^{2} x=\\\\= (sin^{2} x+cos^{2} x)^{2} -\dfrac{1}{2} \cdot 4sin^{2} x\cdot cos^{2} x=1-\dfrac{1}{2} \cdot sin^{2} 2x=1-\dfrac{1}{2} \cdot \dfrac{1-cos4x}{2} =\\\\=1-\dfrac{1-cos4x}{4} =\dfrac{4-1+cos4x}{4} =\dfrac{3+cos4x}{4} .$

Тогда заданный интеграл примет вид:

$\int\limits {\dfrac{dx}{sin^{4}x+cos^{4} x } } =\int\limits {\dfrac{4dx}{3+cos4x} } \,$

Воспользуемся универсальной подстановкой

$z= tg2x$

$2x=arctg z;\\x=\dfrac{1}{2} arctgz;\\\\dx= \dfrac{1}{2}\cdot \dfrac{dz}{1+z^{2} }$

$cos4x = \dfrac{1-z^{2} }{1+z^{2} }$

Тогда получим

$\int\limits {\dfrac{dx}{sin^{4}x+cos^{4} x } } =\int\limits {\dfrac{4dx}{3+cos4x} } \,=\int\limits {\frac{4\cdot\dfrac{1}{2} \cdot \dfrac{dz}{1+z^{2} } }{3+\dfrac{1-z^{2} }{1+z^{2} } } } \, =\int\limits {\dfrac{2dz}{3+3z^{2} +1-z^{2} } } \, =\\\\=\int\limits {\dfrac{2dz}{2z^{2} +4} } \,=\int\limits {\dfrac{2dz}{2(z^{2} +2)} } \,=\int\limits {\dfrac{dz}{z^{2} +2} } \,=\int\limits {\dfrac{dz}{z^{2} +(\sqrt{2})^{2} } } \,=\dfrac{1}{\sqrt{2} } \cdot arctg\dfrac{z}{\sqrt{2} } +C$

Вернемся к подстановке и получим

$\int\limits {\dfrac{dx}{sin^{4}x+cos^{4} x } } =\dfrac{1}{\sqrt{2} } \cdot arctg \dfrac{tg2x}{\sqrt{2} } +C$

При решении были использованы тригонометрические формулы

$sin^{2} x+cos^{2} x=1;\\sin2x=2sinxcosx;\\\\cos2x= \dfrac{1-tg^{2} x}{1+tg^{2}x }$

и неопределенный интеграл

$\int\limits {\dfrac{dx}{x^{2} +a^{2} } } \, =\dfrac{1}{a} arctg \dfrac{x}{a} +C$

#SPJ1