Ответы
Ответ дал:
1
Ответ:
решение смотри на фотографии
Приложения:
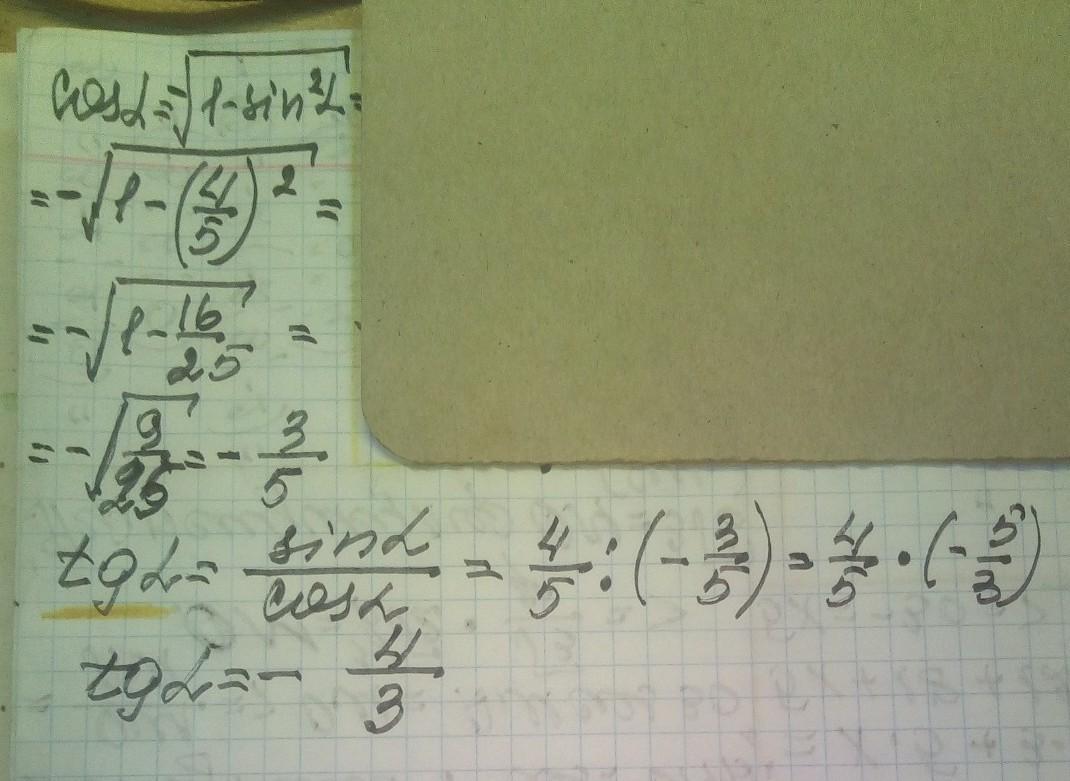
Ответ дал:
2
Ответ:
Так как , то угол находится во 2 четверти, где
,
поэтому .
solka0000:
будь ласка , допоможіть мені з останнім завданням , яке я щойно додала , даю максимум балів
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад