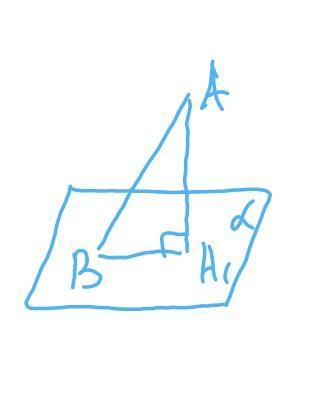
Из точки к плоскости проведена наклонная, длина которой равна 5 см.
Расстояние от точки к плоскости равно 4 см. Найти проекцию этой
наклонной. (С ЧЕРТЕЖОМ ) Даю 20 баллов
BMW52:
Вам же Пеппер решил. Только там нет чертежа.
Можете,пожалуйста, начертить чертежи где отвечали мне на вопрос?
ПО телефона не позволяет делать чертежи.
Вы можете где нет чертежа в ответе поставить нарушение.
Вы не способны нарисовать прямоугольный треугольник? Гипотенуза 5 см, катет 4 см. Вот и весь рисунок.
Не способна
Нет, не такой! Там пространственный чертёж. И Вы, Пеппер должны были помочь и с решением и с чертежом. А Вы схалтурили.
Ответы
Ответ дал:
1
Ответ:
3 см
Объяснение:
АВ =5 см - наклонная
АА1=4 см
Найти : А1В
Решение :
Тр-к АА1В - прямоугольный
По теореме Пифагора :
А1В=корень (АВ²-АА1²) =корень (5²-4²)=
=корень 9=3 см
Приложения:
Ответ дал:
2
Ответ:
3 см.
Объяснение:
Имеем прямоугольный треугольник с катетом 4 см и гипотенузой 5 см. Требуется найти второй катет.
Можно без вычислений, зная что соотношение сторон египетского треугольника равно 3:4:5.
Если катеты 3 см и 4 см, то гипотенуза 5 см; неизвестный катет=3 см.
Можно сделать вычисления по теореме Пифагора:
в²=с²-а²=25-16=9; в=√9=3 см.
Приложения:
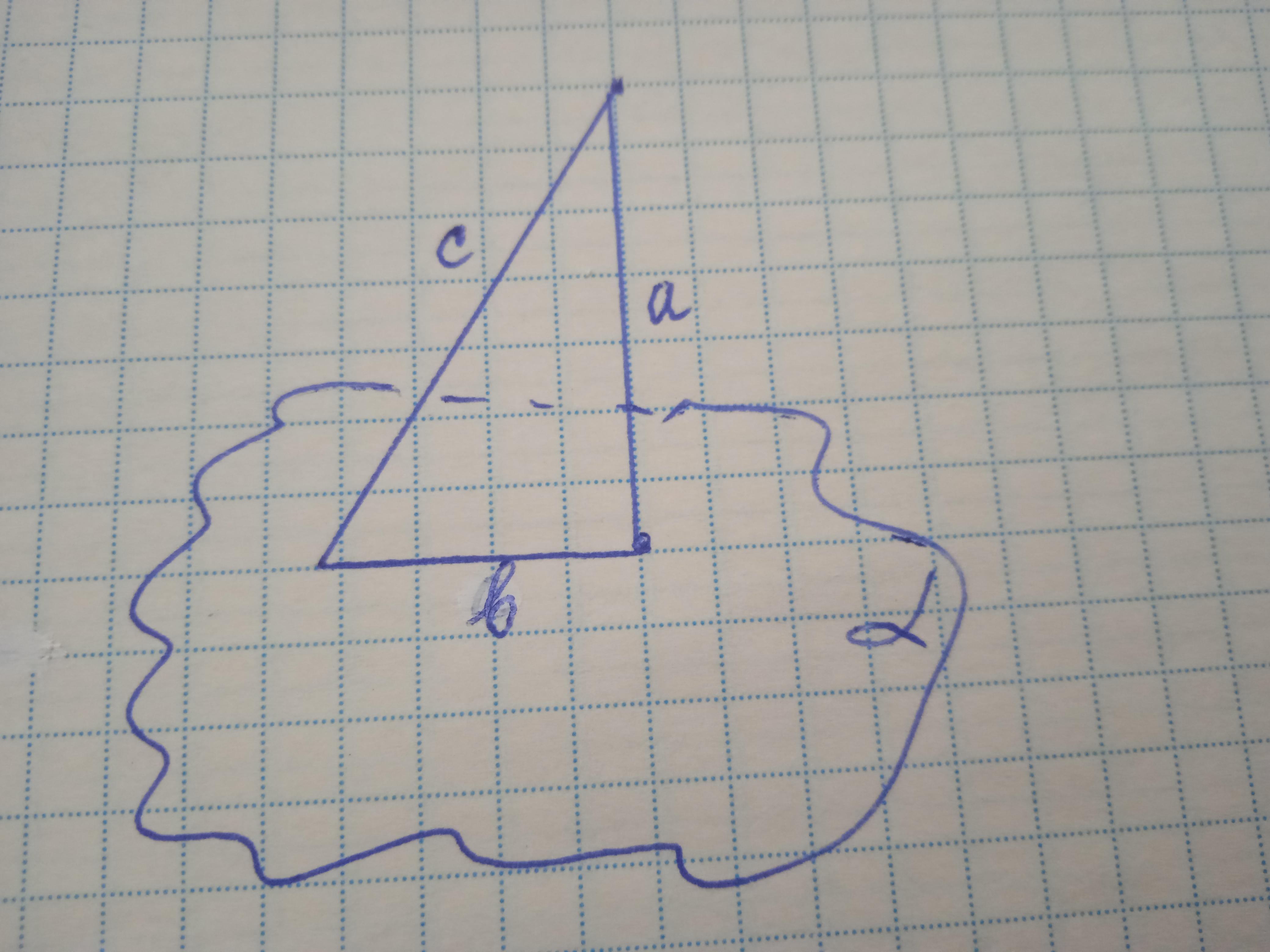
И где плоскость?
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад