Question

Доказать что диагонали АС и ВD перпендикулярны, тогда AD²+BC²=AB²+CD²

Answer 1

Дано:

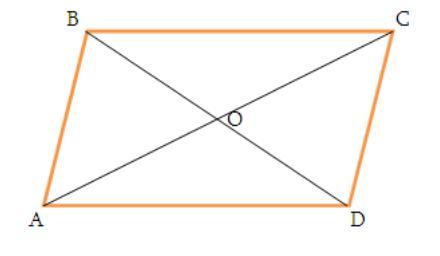
ABCD четырехугольник

АС и ВDдиагонали

доказать что диагонали АС и ВD перпендикулярны

___________________________________________

по рисунку О - точка пересечения диагоналей АС и ВD

поскольку диагонали АС и ВD перпендикулярны ⇔

∠AOD = ∠AOB = ∠BOC = ∠COD = 90°

В прям. треугольниках AOD, AOB, BOC, COD

по теорему Пифагора`

AD² = AO² + OD²

AB² = AO² + BO²

BC² = BO² + OC²

CD² = OC² + OD²

⇔

AD² + BC² = AO² + OD² + BO² + OC²

AB² + CD² = AO² + BO² + OC² + OD²

⇔

AD² + BC² = AB² + CD² = AO² + BO² + OC² + OD²