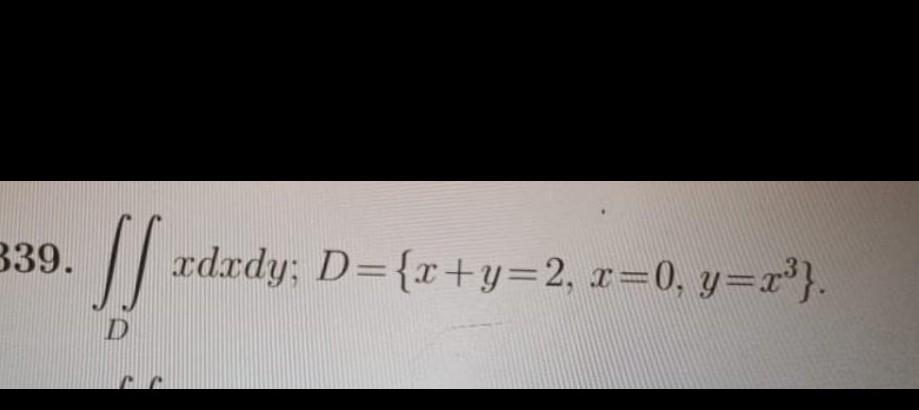Ответы
Ответ дал:
1
Ответ:
7/15
Объяснение:
Делаем чертеж.
х + у = 2 ⇒ у = 2-х
Нам нужен внешний интеграл по х.
Мотрим, как изменяется х.
Он изменяется от 0 до 1.
Как изменяется у.
Он изменяется от x³ до (2-х)
Вот, собственно и все.
Мы перешли от двойного интеграла к повторному.
Вычисляем внутренний интеграл
Теперь считаем внешний интеграл
Приложения:

Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад