Радиус одной из двух внешних касающихся окружности равен 1 расстояние между точками касания их общей касательной равна 6 найдите радиус второй окружности
Ответы
Ответ дал:
0
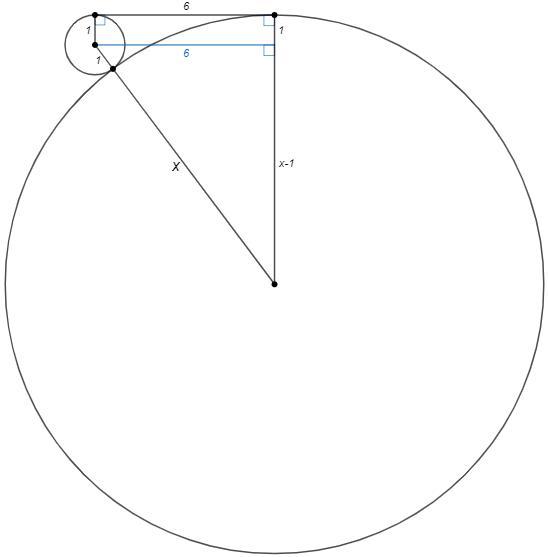
Первый способ.
Опустим перпендикуляр из центра меньшей окружности на радиус большей окружности.
Длина этого перпендикуляра равна расстоянию между точками касания общей касательной, 6.
Получим прямоугольный треугольник с гипотенузой, равной сумме радиусов (x+1) и катетом, равным разности радиусов (x-1)
(x+1)^2 =(x-1)^2 +36 => 4x =36 => x=9
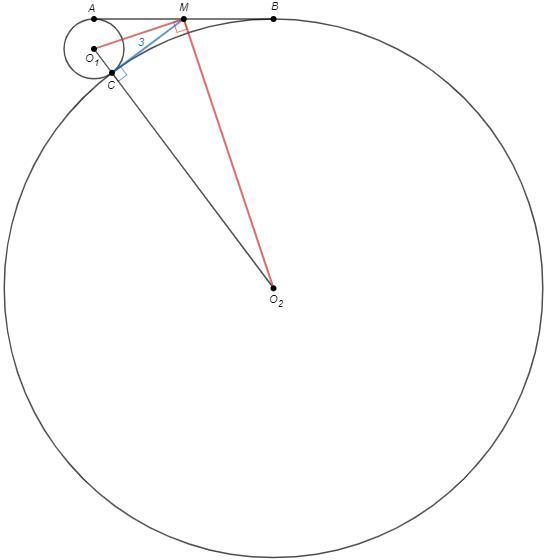
Второй способ.
Проведем вторую общую касательную через точку С.
Она пересечет отрезок AB в точке M.
Отрезки касательных из одной точки равны, MC=MA=MB=3.
MO1 и MO2 - биссектрисы.
Угол между биссектрисами смежных углов - прямой.
Тогда MC - высота из прямого угла.
MC^2 =O1C*O2C => O2C=9
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад