Question

Решить неравенство и выбрать из предложенных наименьшее число

Answer 1

Ответ:

$25^{x}\geq 5^{x+1}+24\ \ \ \Rightarrow \ \ \ \ (5^{x})^2-5\cdot 5^{x}-24\geq 0\ \ ,\\\\t=5^{x} > 0\ \ ,\ \ \ \ t^2-5t-24\geq 0\ \ ,\ \ \ t_1=-3\ ,\ t_2=8\ \ (teorema\ Vieta)\\\\(t+3)(t-8)\geq 0$  

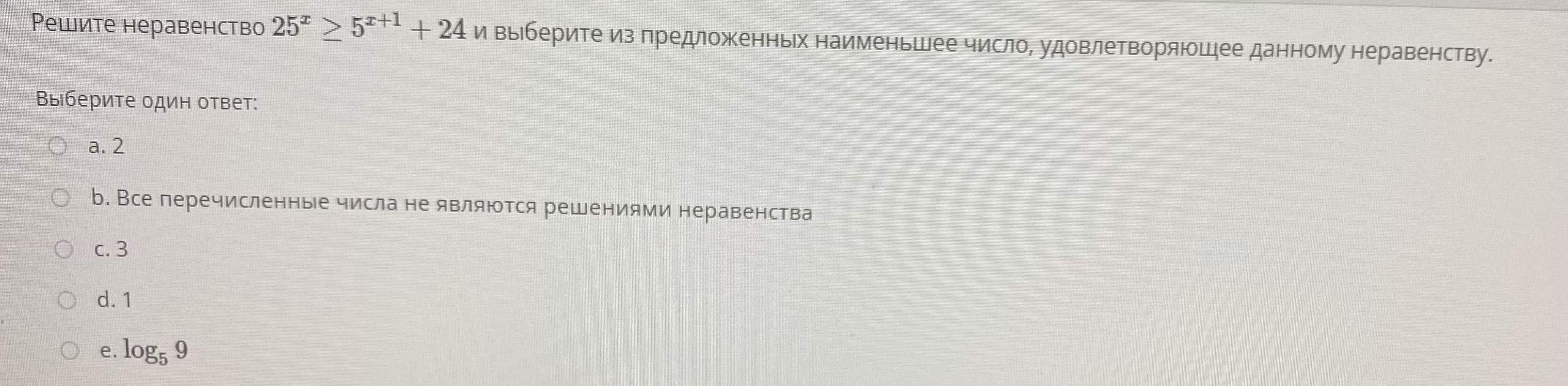
Решаем неравенство методом интервалов .

Нули функции  t= -3  и  t=8 . Отметим эти числа на оси .  Подсчитаем знаки в образовавшихся интервалах . И выберем те интервалы, где записан знак плюс . Учтём, что неравенство нестрогое, значит граничные точки будут включаться в решение .

$+++[-3\, ]---[\ 8\ ]+++\ \ \ \ \ \ t\in (-\infty ;-3\ ]\cup [\ 8\ ;+\infty \, )$  

Учитывая, что  t > 0 , выбираем только второй промежуток .

$t\in [\ 8\ ;+\infty \, )\ \ \Rightarrow \ \ \ \ \ 5^{x}\geq 8\ \ ,\ \ 5^{x}\geq 5^{log_58}$  

Так как показательная функция с основанием, большим 1 , возрастающая, то знак между аргументами функций будет таким же, как и знак между самими функциями .

 $x\geq log_5\, 8\\\\\boldsymbol{Otvet:\ \ x\in [\ log_5\, 8\ ;+\infty \, )}\ .$  Наименьшее из предложенных чисел из указанного промежутка равно  $\bf log_5\, 9$ ,  так как  $log_5\, 8\approx 1,292$  ,  

$log_5\, 9\approx 1,365$  .  

Можно сравнить так:   $5 < 8 < 9 < 25\ \ \ \Rightarrow$    

                                    $\underbrace{log_55}_{1} < log_58 < log_59 < \underbrace{log_525}_{2}$