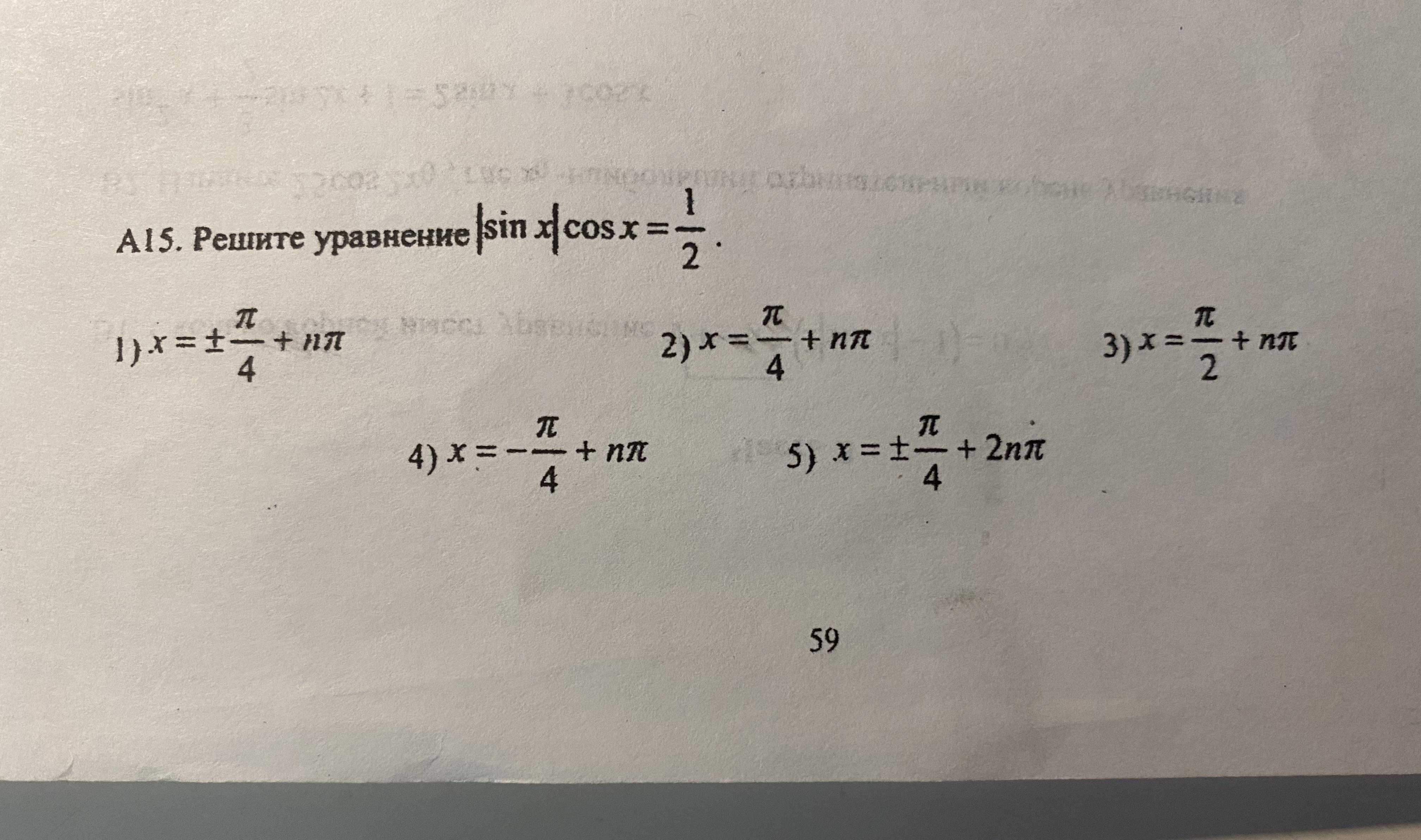Ответы
Ответ дал:
1
Ответ:
5)
Пошаговое объяснение:
Если получаем уравнение
при этом удовлетворяют условию
а
— не удовлетворяют.
Если аналогично:
Из найденных корней только удовлетворяет условию
Таким образом, решения нашего уравнения
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад