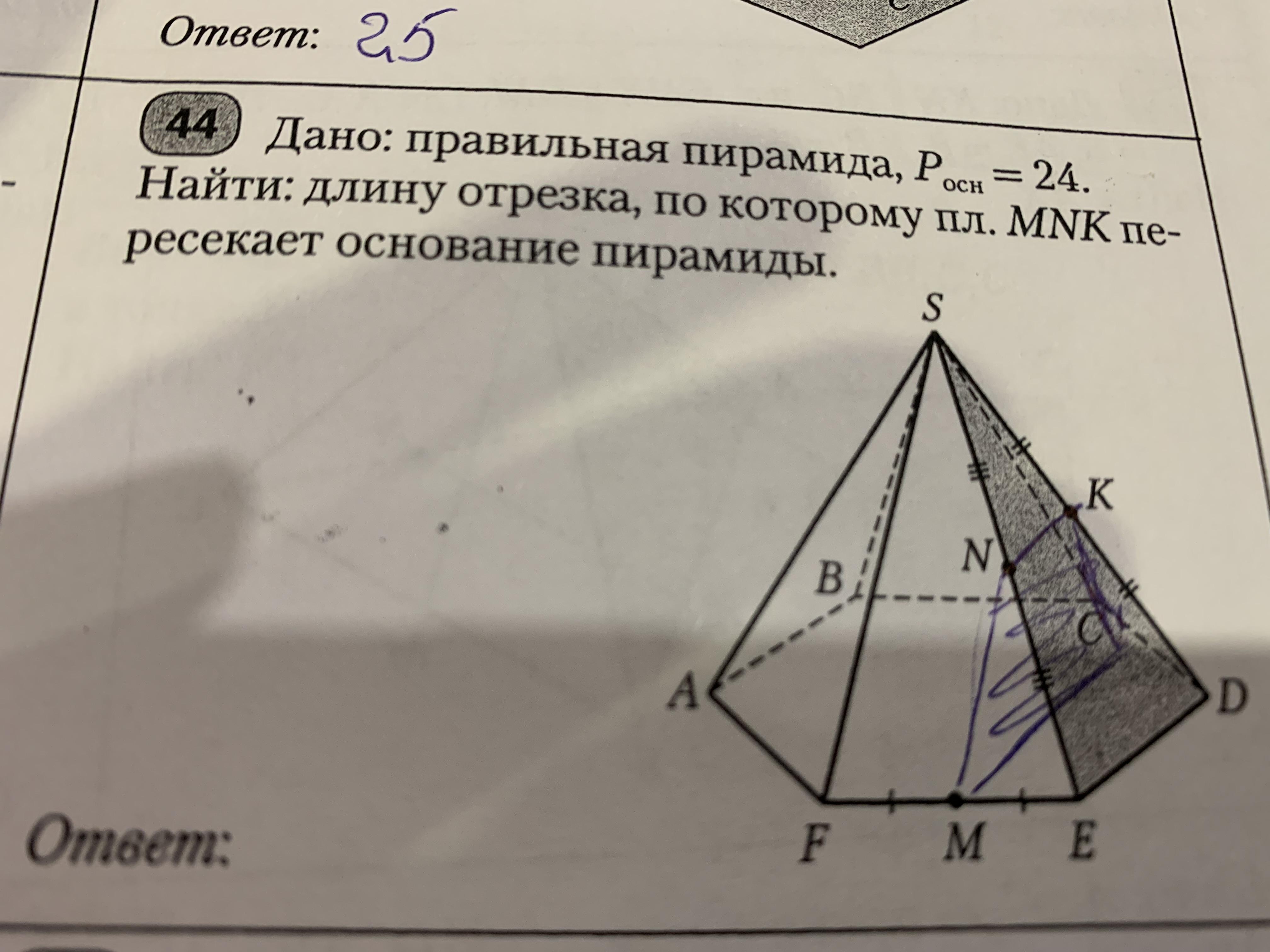
Дано: правильная пирамида, Р осн=24. Найти: длину отрезка, по которому пл.MNK пересекает основание пирамиды
Приложения:
Ответы
Ответ дал:
2
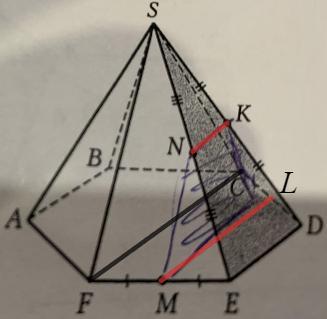
KN - средняя линия в DSE => KN||DE
Прямая KN параллельна прямой DE, лежащей в плоскости основания, следовательно параллельна основанию.
Плоскость MNK проходит через прямую KN, параллельную основанию, тогда LM (линия пересечения MNK и основания) параллельна KN.
LM||KN||DE
В основании правильной шестиугольной пирамиды - правильный шестиугольник.
CDEF - трапеция, DE=24/6=4, CF=2DE=8
LM - средняя линия CDEF => LM =(DE+CF)/2 =6
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад