Question

Найдите высоту цилиндра наибольшего объема, который можно вписать в шар радиуса 1.​

Answer 1

Ответ:

$\frac{{2\sqrt 3 }}{3}$

Пошаговое объяснение:

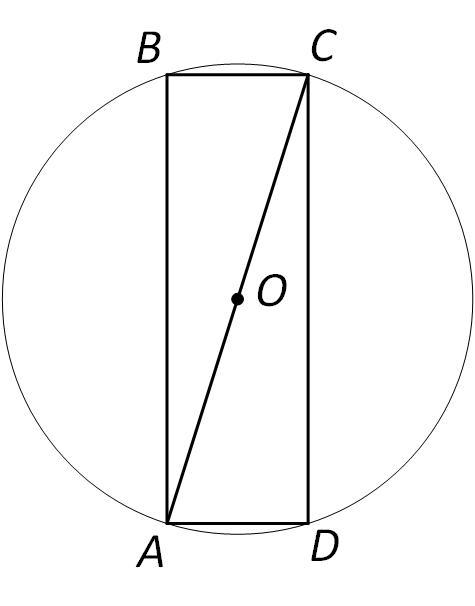
Рассмотрим осевое сечение. По условию $AC = 2 \cdot 1 = 2.$ Пусть высота цилиндра $CD = h = x,$ тогда из прямоугольного треугольника $ACD$ по теореме Пифагора $AD = \sqrt {{2^2} - {x^2}} = \sqrt {4 - {x^2}} .$ Отсюда радиус основания цилиндра $r = \frac{{AD}}{2} = \frac{{\sqrt {4 - {x^2}} }}{2}.$

Объем цилиндра $V = \pi {r^2}h = \pi {\left( {\frac{{\sqrt {4 - {x^2}} }}{2}} \right)^2} \cdot x = \pi \left( {\frac{{4 - {x^2}}}{4}} \right)x = \pi x - \frac{\pi }{4}{x^3}.$

Найдем производную от объема пользуясь дважды формулой $({x^n})' = n{x^{n - 1}}.$

$V'(x) = \pi - \frac{{3\pi }}{4}{x^2}.$

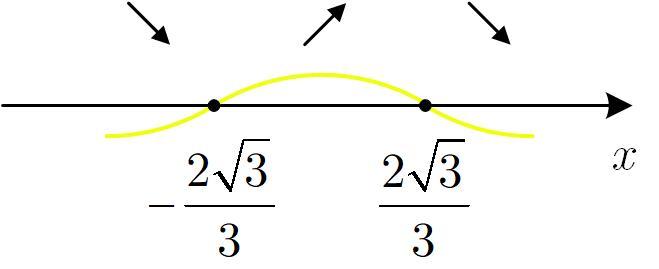
Уравнение $V'(x) = 0$ имеет корни $x = \pm \frac{{2\sqrt 3 }}{3}.$ С помощью метода интервалов убеждаемся, что точка $x = \frac{{2\sqrt 3 }}{3}$ является точкой максимума функции $V(x).$