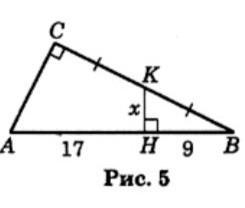
У прямокутному трикутнику АСВ відрізок КН перпен- дикулярний до гіпотенузи AB. CK = KB, AH = 17 см, НВ = 9 см. Знайдіть відрізок НК (рис. 5).
Приложения:
Ответы
Ответ дал:
0
Ответ:
Объяснение:
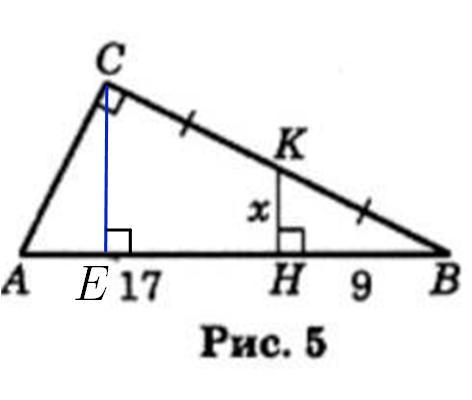
Опустим из точки высоту
на гипотенузу. Тогда
будет средней линией в треугольнике
,
Так как по формуле то
значит
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
9 лет назад