Question

Точка касания кружности, вписанной в ромб, делит сторону ромба на отрезки 2 и 18. Найдите радиус окружности.

Answer 1

Ответ:

R=6 (см)

Пошаговое объяснение:

АВ=АК+КВ=18+2=20 (см)

Свойства касательной: отрезки касательных к окружности, проведенных из одной точки, равны ⇒

ВК=ВМ=2 (см),     АК=АР=18 (см)

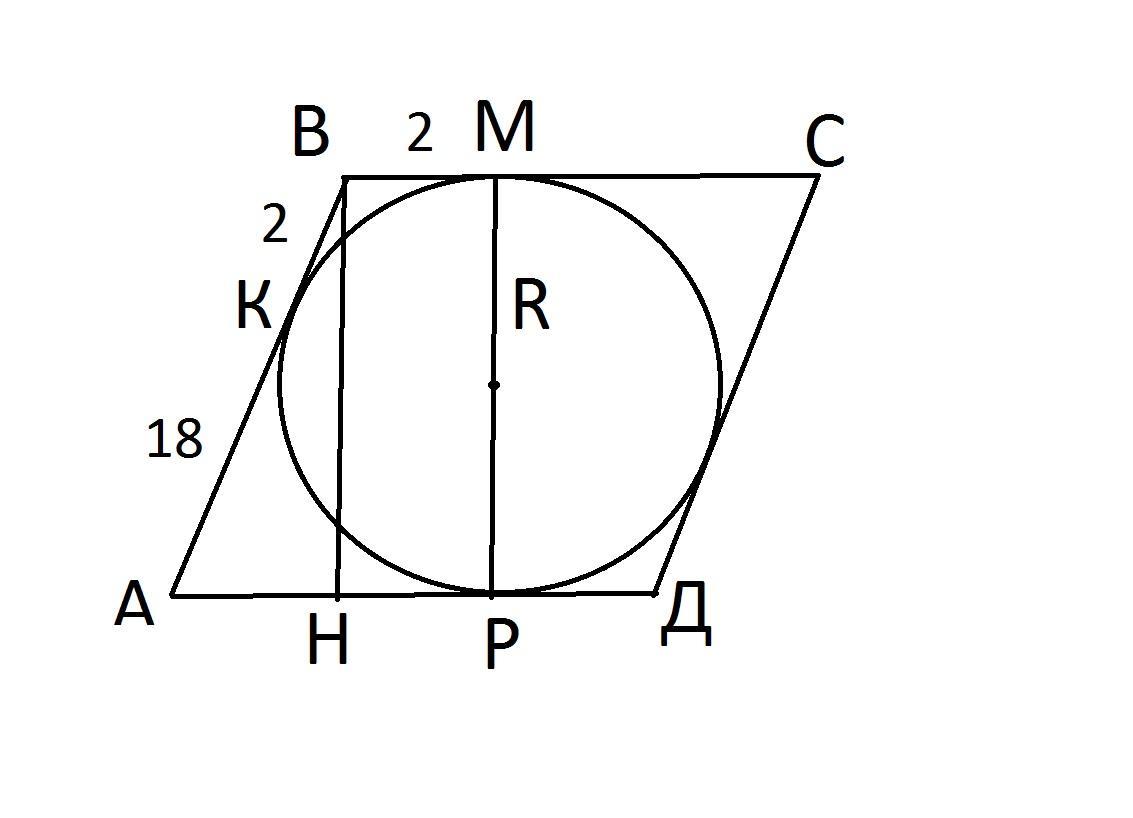
Проведем высоту ВН и диаметр МР (ВН=МР)

следовательно ВМ=НР=2 (см)

АН=АР-НР=18-2=16 (см)

По теореме Пифагора:

ВН=√(АВ²-АН²)=√(20²-16²)=√(400-256)=√144=12 (см)

Так как высота ВН равняется диаметру МР, следовательно:

R=BH/2=12/2=6 (см)