50 БАЛЛОВ ГЕОМЕТРИЯ!

Приложения:

Ответы

Ответ дал: natalyabryukhova

Ответ:

Расстояние от точки пересечения диагоналей прямоугольника до его большей стороны равно 1,5 см.

Объяснение:

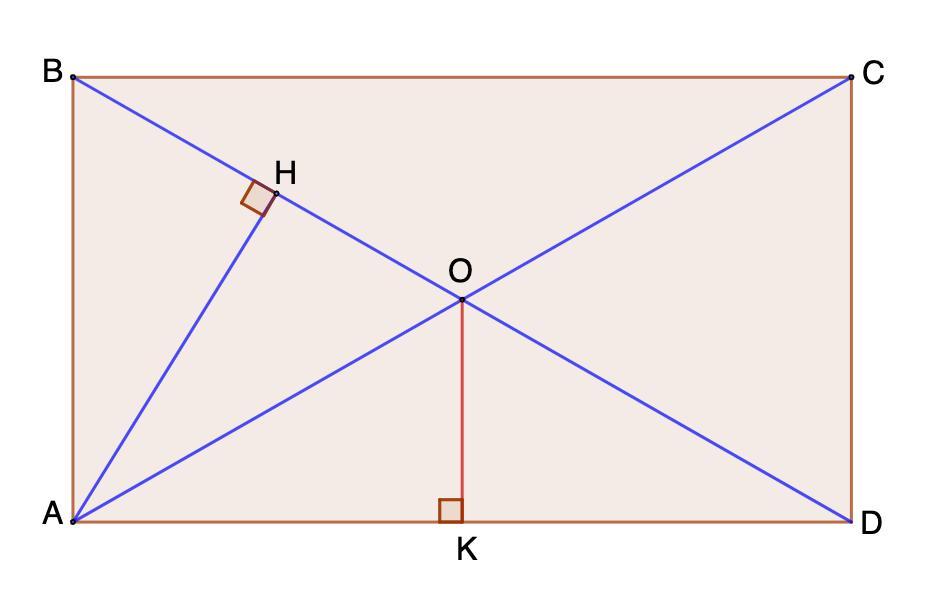
14. Перпендикуляр, опущенный с вершины А прямоугольника ABCD на диагональ, делит ее в отношении 1:3, считая от вершины В. Найти расстояние от точки пересечения диагоналей прямоугольника до его большей стороны, если длина диагонали 6 см.

Дано: ABCD - прямоугольник;

BD и AC - дтагонали; BD ∩ AC = О;

АН ⊥ BD; BH : HD = 1 : 3.

BD = 6 см.

Найти: расстояние от точки пересечения диагоналей прямоугольника до его большей стороны.

Решение:

Расстояние от точки до прямой есть длина перпендикуляра, опущенного из данной точки на данную прямую.

⇒ ОК ⊥ AD.

⇒ Искомый отрезок ОК.

1. Пусть ВН = х см, тогда HD = 3x см, а BD = 4x см.

Диагонали прямоугольника равны и точкой пересечения делятся пополам.

⇒ АС = BD = 4х = 6 см;

AO = OC = BO = OD = 2x = 6 : 2 = 3 (см)

2. Рассмотрим ΔАВО.

АН ⊥ ВО (условие) ⇒ АН - высота;

АН = х см; НО = 2х - х = х (см) ⇒ АН - медиана.

Если в треугольнике высота является медианой, то этот треугольник равнобедренный.

⇒ АВ = АО = 3 см.

3. Рассмотрим ΔABD - прямоугольный.

ОК ⊥ AD.

Если две прямые перпендикулярны третьей, то они параллельны между собой.

⇒ OK || AB.

BO = OD

Если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

⇒ ОК - средняя линия ΔABD;