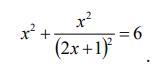Ответы
Ответ дал:
1
Ответ:
Объяснение:
Сделаем замену
Тогда
откуда
Получаем уравнение
Делаем обратную замену:
1)
2)
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад