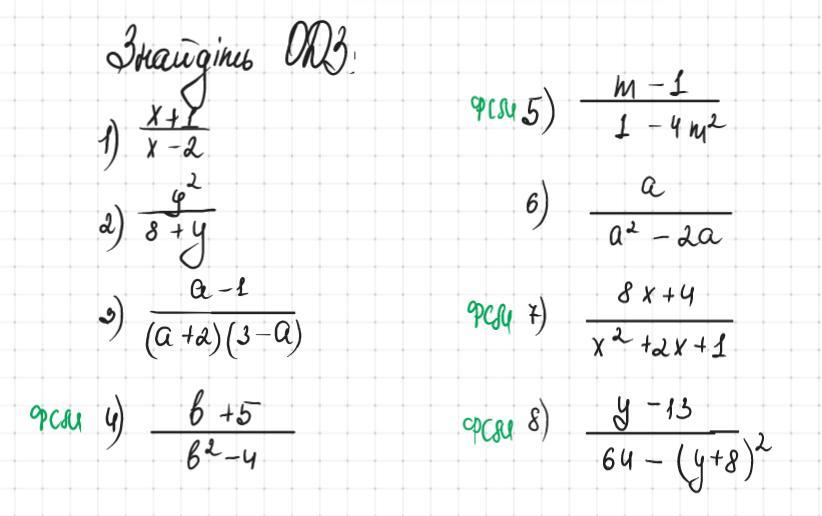Ответы
Ответ дал:
1
1) x-20
x2
2) y+80
y-8
3) a+20 a
-2
3-a0 a
3
4) -4=(b-2)(b+2)
0
b+20 b
-2
b-20 b
2
5) 1-4=(1-2m)(1+2m)
0
1+2m0 m
1-2m0 m
6) -2a=a(a-2)
0
a0
a-20 a
2
7) +2x+1=
0
x-1
8) 64-=(8-y-8)(8+y+8)=-y(16+y)
0
y0
16+y0 y
-16
Ответ дал:
1
Ответ:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад