Question

Помогите с первым заданием

Answer 1

Ответ:

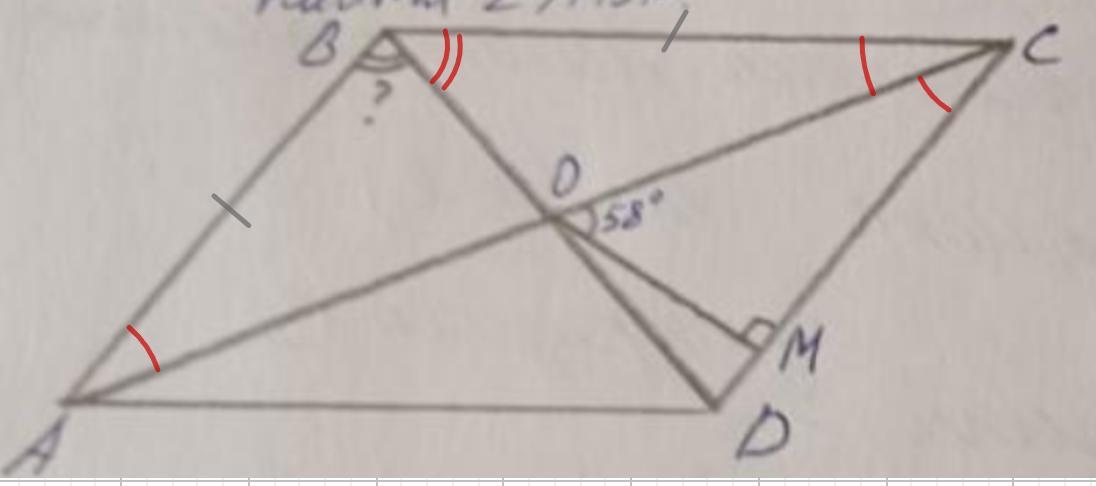
Угол ABD равен 58°.

Объяснение:

1. ABCD - параллелограмм. АВ = ВС, ОМ ⊥ DC, ∠СОМ = 58°. Найти ∠ABD.

Дано: ABCD - параллелограмм;

АВ = ВС,

ОМ ⊥ DC,

∠СОМ = 58°.

Найти: ∠ABD.

Решение:

1. ABCD - параллелограмм;

АВ = ВС (условие)

• Противоположные стороны параллелограмма равны.

⇒ AB = BC = CD = AD

⇒ ABCD - ромб.

2. Рассмотрим ΔМОС - прямоугольный.

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠ОСМ = 90° - 58° = 32°

3. Рассмотрим ΔАВС - равнобедренный.

• При пересечении двух параллельных прямых третьей накрест лежащие углы равны.

⇒ ∠ВАС = ∠АСВ = 32°

• Углы при основании равнобедренного треугольника равны.

⇒ ∠ВАС = ∠ВСА = 32°

• Сумма углов треугольника равна 180°.

⇒ ∠В = 180° - (32° + 32°) = 116°

• Диагонали ромба являются биссектрисами его углов.

⇒ ∠АВD = 116° : 2 = 58°

Угол ABD равен 58°.