Обчисли третю сторону трикутника, якщо дві його сторони дорівнюють 7 і 8 см відповідно, а кут між ними дорівнює 60°
Ответы
Ответ дал:
23
Ответ:
√57 см
Объяснение:
теорема косинусов:
с=√(а²+b²-2*a*b*cos∠(ab);
a=7см; b=8см; ∠(аb)=60°
cos60°=½
c=√(7²+8²-2*7*8*½)=√(49+64-56)=
=√57 см
rubkub31:
помогите
прошу очень срочно
ахахаха было 5 звёзд а я сделал 3.7
Смешно, обхохочешься...
согл
https://znanija.com/task/49961741?utm_source=android&utm_medium=share&utm_campaign=question помогите пожалуйста, очень надо, дам 30 баллов
kula ma ka Pūnaewele ʻAʻole hiki iaʻu ke kiʻi aku iā ʻoe ma ke kelepona ʻaʻole hiki iaʻu ke kiʻi aku iā ʻoe ma ke kelepona ʻAʻole maopopo iaʻu ke ʻano aia wau i loko o kahi huna huna ʻaʻole wau ʻike pehea e hana ai. ma keia hihia aole au i ike
ггсгнк
Здравствуйте вы не могли бы мне помочь с математикой очень нужно
помогите пожалуйста очень срочно даю 30 балов укр. мова
Ответ дал:
22
Ответ:
Сторона треугольника равна см
Объяснение:
Дано: AB = 7 см, BC = 8 см, ∠ABC = 60°
Найти: AC - ?
Решение:
По следствию из теоремы косинусов для треугольника ΔABC:
см.
Приложения:
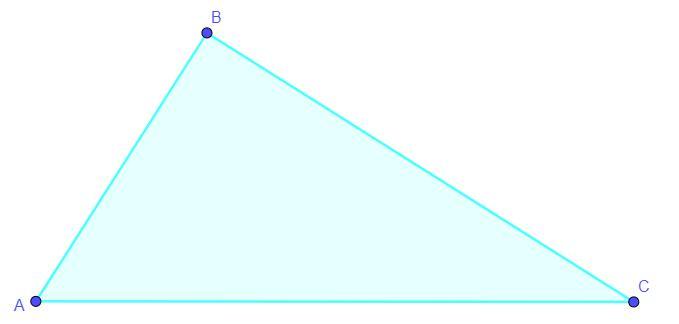
помогите пожалуйста с задачей
Амогус
Аммооогггуууссс
опр
Нащо, ви все це пишите?
привет✋ маган кумек Тесындершы утыныш агылшын дан
Так. Усім привіт. Нічого не зрозуміло, але дуже цікаво....
помогите пожалуйста очень срочно даю 30 балов укр. мова
Помогите мне пожалуйста
Вам вже павук відповідає.
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад