Question

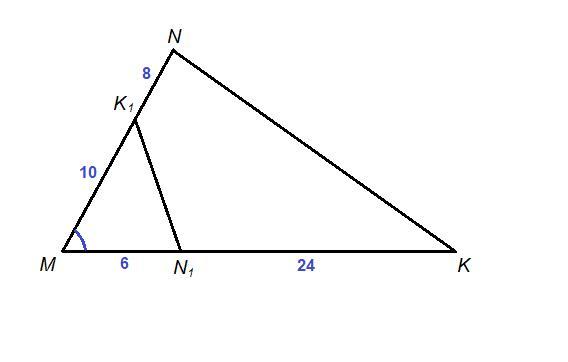
На сторонах МК и MN треугольника MKN отмечены соответственно точки И1 и К1. Известно, что MN1= 6 см, N1K = 24 см, MK1 = 10 см, K1N = 8см. Докажите, что треугольники МNK и MN1K1 Подобны.

Answer 1

Ответ:

Треугольник МNK - равнобедренный (MN=NK по условию). Следовательно, см=2 к по свойству

равнобедренного треугольника.

МА=KB (дано). → Δ ΑΜΚ=Δ ΒΜΚ πο

двум сторонам ( AM=ВК и МК - общая)

и углу между ними (угол M=K)

∆ АМК=ВКМ по первому признаку равенства треугольников. В равных треугольниках против равных углов лежат равные стороны. АК=МВ=3 см.

Answer 2

Ответ:

Треугольник MNK подобен треугольнику MN₁K₁ по второму признаку.

Объяснение:

Второй признак подобия треугольников:

• если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами, равны, то треугольники подобны.

MK = MN₁ + N₁K = 6 + 24 = 30 см

MN = MK₁ + K₁N = 10 + 8 = 18 см

Найдем отношение сторон:

$\dfrac{MN_1}{MN}=\dfrac{6}{18}=\dfrac{1}{3}$

$\dfrac{MK_1}{MK}=\dfrac{10}{30}=\dfrac{1}{3}$

$\dfrac{MN_1}{MN}=\dfrac{MK_1}{MK}$

Итак, в треугольниках MNK и MN₁K₁ две стороны пропорциональны, а угол между ними - ∠М - общий, тогда треугольник MNK подобен треугольнику MN₁K₁ по второму признаку.