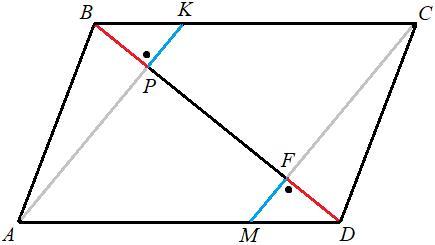
На сторонах BC і AD чотирикутника ABCD позначено точки K і M відповідно. Відрізок AK перетинає діагональ BD у точці P, а відрізок CM - у точці F. Відомо, що AK || CM, PK = FM, B = FD, KC = AM. Доведіть, що кут BAD = куту BCD
15 баллов
Ответы
Ответ дал:
1
На сторонах BC и AD четырехугольника ABCD обозначены точки K и M соответственно. Отрезок AK пересекает диагональ BD в точке P, а отрезок CM - в точке F. Известно, что AK || CM, PK=FM, BP=FD, KC=AM. Докажите, что ∠BAD=∠BCD.
∠BPK=∠DFM (внешние накрест лежащие при AK||CM)
△BPK=△DFM (по двум сторонам и углу между ними)
=> ∠PBK=∠FDM, BK=DM
BC =BK+KC =DM+AM =AD
△DBC=△BDA (по двум сторонам и углу между ними, BD - общая)
=> ∠BCD=∠BAD
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад