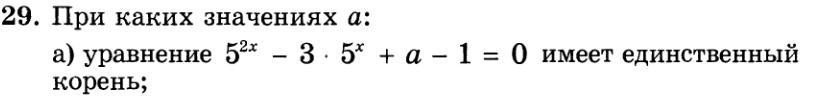Ответы
Ответ дал:
1
Ответ:
При а = 3,25
Пошаговое объяснение:
При каких значениях а :
Уравнение 5²ᕁ -3 · 5ᕁ + а - 1 = 0 имеет единственный корень;
Перепишем уравнение :
Первое , что нам пришло бы в голову , это замена 5ᕁ = t , так и заменим :
Нам это напоминает квадратное уравнение вида x² + px + q = 0 , но в данном случае у нас вместо "a - 1" это целое q , следущим образом мы бы перешли к дискриминанту:
По условию нам нужно найти такое а , при котором уравнение будет иметь один корень , но квадратное уравнение имеет один корень только тогда , когда D = 0 , следовательно ,значение дискриминанта приравним к нулю :
При a = 3,25 уравнение 5²ᕁ -3 · 5ᕁ + а - 1 = 0 имеет единственный корень;
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад