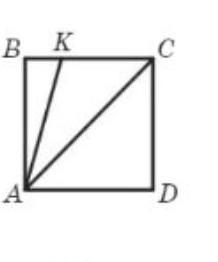
На стороні ВС квадрата ABCD (рис. 52) позна- чили точку К так, що АКВ = 74°. Знайдіть кут САК.
Приложения:
zmeura1204:
Де рис. 52?
Ответы
Ответ дал:
1
Ответ:
29°
Объяснение:
АС- діагональ квадрата є бісектриса кута.
∠КСА=∠ВСD/2=90°/2=45°
∠AKB- зовнішній кут трикутника ∆АКС;
∠АКВ=∠КСА+∠САК, теорема зовнішнього кута.
∠САК=∠АКВ-∠КСА=74°-45°=29°
Ответ дал:
0
Ответ: ∡CAK =29°
Объяснение:
Рассмотрим ΔАВК . ∡ВАК= 90°-∡ВКА = 90°-74°=16°
АС - диагональ квадрата => AC биссектриса ∡А => ∡BAC =45°
=> ∡ KAC= ∡BAC -∡BAK= 45°-16°=29°
Вас заинтересует
2 года назад
2 года назад
7 лет назад