Ответы
Відповідь:
а + в = 100 единиц.
Пояснення:
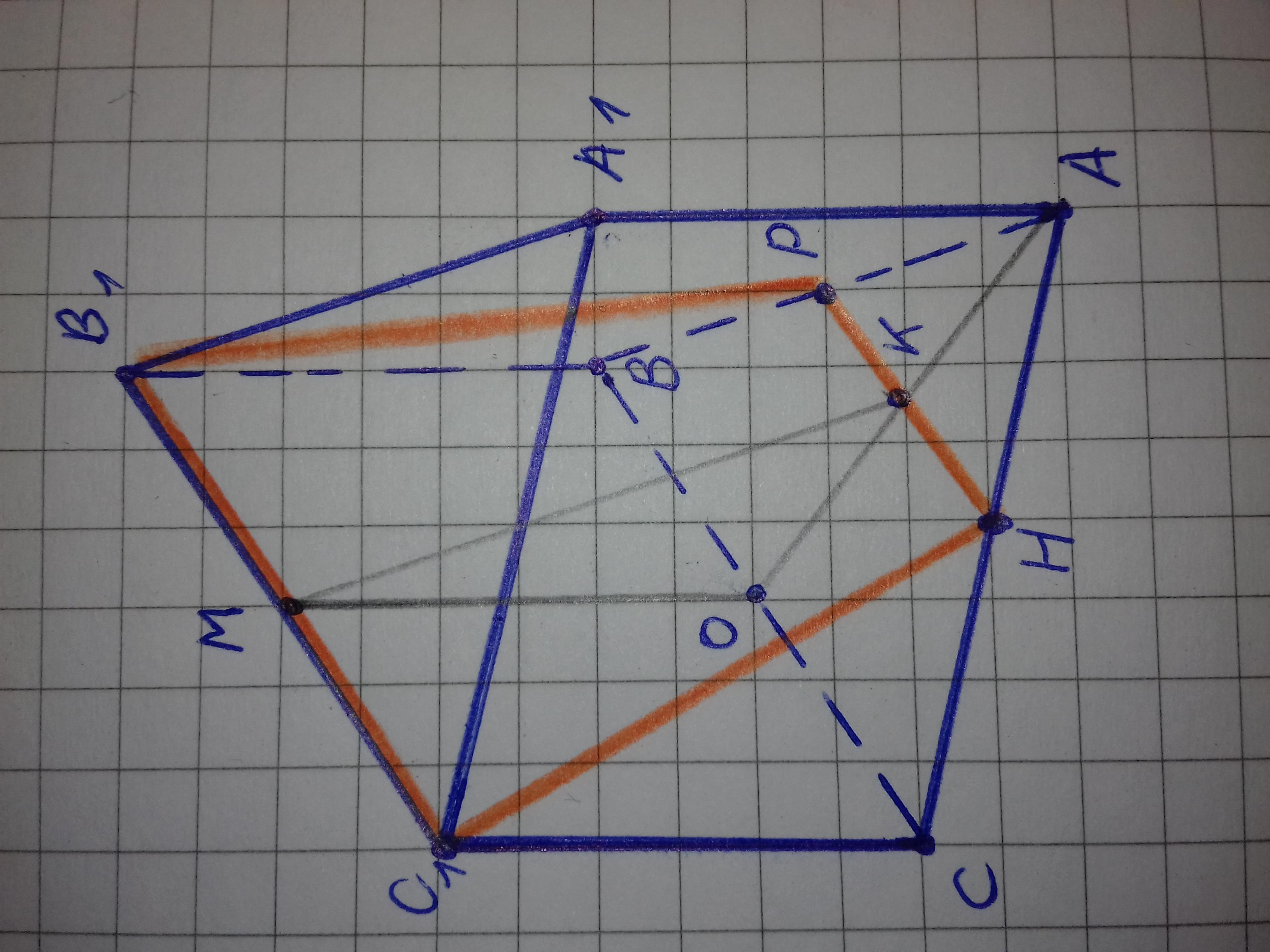
Плоскости АВС и А1В1С1 - параллельны. Следовательно секущая плоскость В1С1Р пересечет эти две плоскости по параллельным линиям. Проводим через точку Р прямую параллельную В1С1 и получаем на ребре АС точку Н. Поскольку исходная призма правильная, то треугольники АВС и А1В1С1 - равносторонние, точка Н - середина ребра АС, а отрезок РН - средняя линия треугольника АВС.
РН = ВС / 2 = 12 / 2 = 6 единиц.
Мы получили сечение правильной призмы АВСА1В1С1 плоскостью В1С1Р - трапецию РНС1В1. Найдем её площадь.
В равносторонних треугольниках все углы равны 60°, следовательно высота АО треугольника АВС равна:
АО = АС × sin ( 60° ) = 12 × √3 / 2 = 6 × √3 единиц.
Поскольку РН - средняя линия треугольника АВС, то ОК - половина высоты АО:
ОК = АО / 2 = 6 × √3 / 2 = 3 √3 = √27 единиц.
ОМ равна высоте призмы:
ОМ = 8 единиц.
По теореме Пифагора находим МК:
МК = √ ( ОМ² + ОК² ) = √ ( 8² + √27² ) = √ ( 64 + 27 ) = √91
Площадь трапеции равна произведению полусуммы оснований на высоту:
S = ( РЕ + В1С1 ) / 2 × МК = ( 6 + 12 ) / 2 × √91 = 9 × √91 единиц в квадрате.
По условию задачи площадь надо представить в виде S = а × √в, где в - простое число.
а = 9 единиц.
в = 91 единица.
Ответ надо дать в виде а + в.
а + в = 9 + 91 = 100 единиц.