Ответы
Ответ дал:
1
Ответ:
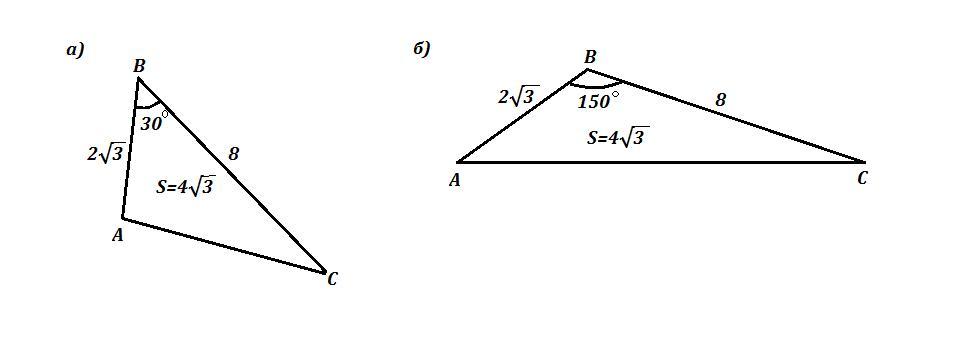
Дан ΔАВС , АВ=2√3 см , ВС=8 см . АС=R .
Найти : АС , S(ΔАВC) .
2) Известна формула площади треугольника через радиус описанной окружности: .
С другой стороны площадь треугольника можно выразить через
синус угла треугольника : .
Угол может быть либо острым , , либо тупым ,
.
1а) . Найдём третью сторону треугольника по теореме косинусов .
см²
1б)
см²
Ответ: 1) см или
cм ;
2) см² .
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
