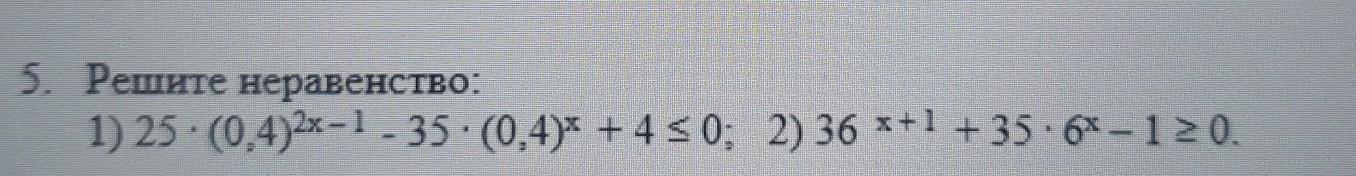Ответы
Ответ дал:
2
Ответ:
1)x∈[1;2]
2)x∈[-2;+∞)
Пошаговое объяснение:
Запишем в виде произведения чисел с одинаковыми основаниями:
Введем замену 0,4ˣ = t
Вернёмся к замене:
Ответ:
Аналогично первому примеру:
Заметим , что 36ˣ можно представить как 6²ˣ:
И только к этому мгновенью можно ввести замену 6ˣ = t
Обратная замена:
Ответ:
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад