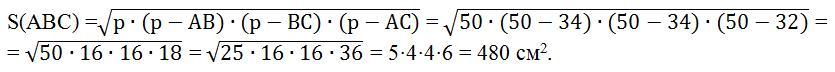У рівнобедреному трикутнику бічна сторона точкою дотику
вписаного кола ділиться на відрізки 18 і 16 см, починаючи від вершини.
Обчислити площу трикутника
Ответы
Ответ:
S(ABC) = 480 см²
Пошаговое объяснение:
Перевод: В равнобедренном треугольнике боковая сторона точкой соприкосновения вписанной окружности делится на отрезки 18 и 16 см, начиная от вершины. Вычислить площадь треугольника.
Нужно знать:
1. Свойство касательных: Отрезки, соединяющие вершины треугольника с точками касания вписанной окружности, равны.
2. Формулу Герона для треугольника.
Дано: ΔABC
AB = BC
ΔABC∩ω = {D; E; F}
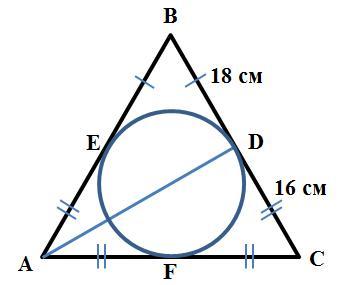
BD = 18 см
DC = 16 см
Найти: S(ABC).
Решение. Треугольник равнобедренный и поэтому:
BC = BD+DC = 18+16 = 34 см = AB.
По свойству касательных
AE = AF, BE = BD, CD = CF (см. рисунок 1).
В силу этого находим:
AC = AF+CF = AE+CD = 16+16 = 32 см.
Полупериметр p:
p = (AB+BC+AC)/2 = (34+34+32)/2 = 100/2 = 50 см.
Далее, вычислим площадь треугольника ABC по формуле Герона (см. рисунок 2).
#SPJ1