Ответы
Ответ дал:
1
Ответ:
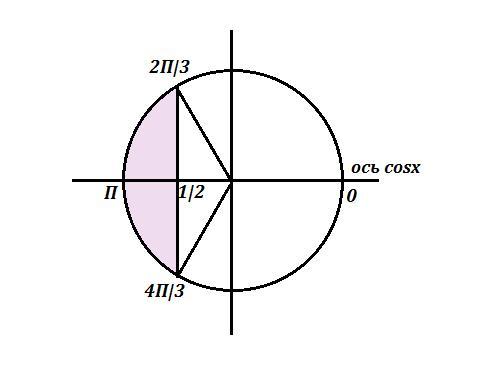
Имеем квадратное неравенство относительно функции .
Знаки функции:
Учитывая, что , получим
.
Вернёмся к старой переменной.
Ответ: .
Приложения:
karimtaichik:
ок
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
8 лет назад