Точка О удалена от вершин прямоугольного треугольника ABC с катетами AB = 7 см и AC = 24 см на расстояние 12,75 Найдите расстояние от точки О до плоскости ABC. (желательно с чертежом)
Ответы
Ответ дал:
0
Объяснение:
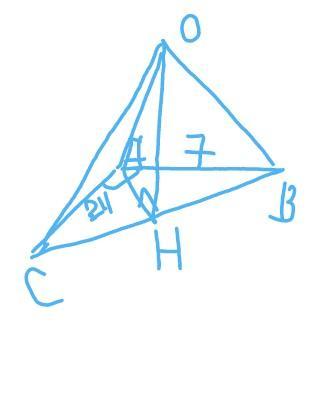
∆АВС ; ∠А=90° ; О∉АВС;
ОС=ОА=ОВ=12,75 см; АВ=7 см; АС=24 см ;
найти: ОН
решение:
по условию ОС=ОА=ОВ ,то и их проекции равны ,т.е СН=ВН=АН .
АН является медианой.
По теореме Пифагора:
СВ=√(АС²+АВ²)=√(24²+7²)=√625=25 см
АН=СН=ВН=СВ:2=25:2=12,5 см
∆ОНА- прямоугольный: ∠Н=90°
по теореме Пифагора:
ОН=√(ОА²-АН²)=√(12,75²-12,5²)=√6,3125 ≈
≈2,5125 см.
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад