помогите пожалуйста
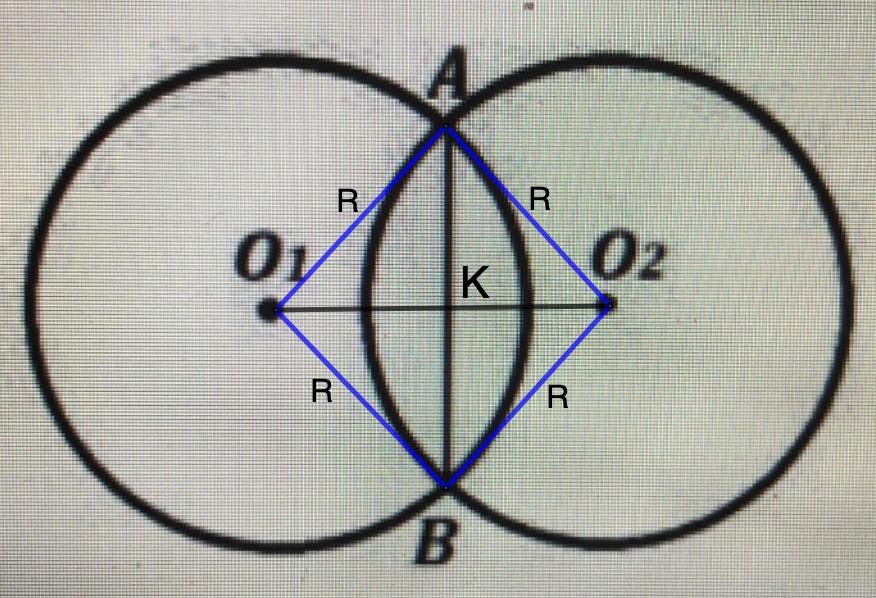
Про окружности на рисунке 4 известно, что они имеют равные радиусы. Докажите, что отрезок, соединяющий центры окружностей, делит АВ пополам.
Приложения:

siestarjoki:
AO1BO2 - ромб. Диагонали ромба точкой пересечения делятся пополам.
Но это верно для любых радиусов: линия центров перпендикулярна общей хорде и делит ее пополам.
Ответы
Ответ дал:
1
Ответ:
Доказано, что отрезок, соединяющий центры окружностей, делит АВ пополам, то есть АК = КВ.
Объяснение:
Про окружности на рисунке 4 известно, что они имеют равные радиусы. Докажите, что отрезок, соединяющий центры окружностей, делит АВ пополам.
Дано: Окр.(О₁ ,R) ∩ Окр.(О₂, R) в точках А и В;
О₁О₂ ∩ АВ = К
Доказать: АК = КВ.
Доказательство:
Рассмотрим О₁АО₂В.
АО₂ = О₁В = R; O₁A = BO₂ = R
- Если в четырехугольнике противоположные стороны попарно равны, то данный четырехугольник - параллелограмм.
⇒ О₁АО₂В - параллелограмм.
- Если в параллелограмме все стороны равны, то это ромб.
⇒ О₁АО₂В - ромб.
- В ромбе диагонали взаимно перпендикулярны и точкой пересечения делятся пополам.
⇒ АК = КВ.
#SPJ1
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад