Question

помогите пожалуйста даю 20 балов

Answer 1

Ответ:

Площадь общей части двух кругов:

$\boldsymbol{\boxed{S = \dfrac{5\pi }{6} - \sqrt{3}}}$ см²

Примечание:

По формуле приведения:

$\boxed{\sin \alpha = \sin (180^{\circ} - \alpha )}$

Объяснение:

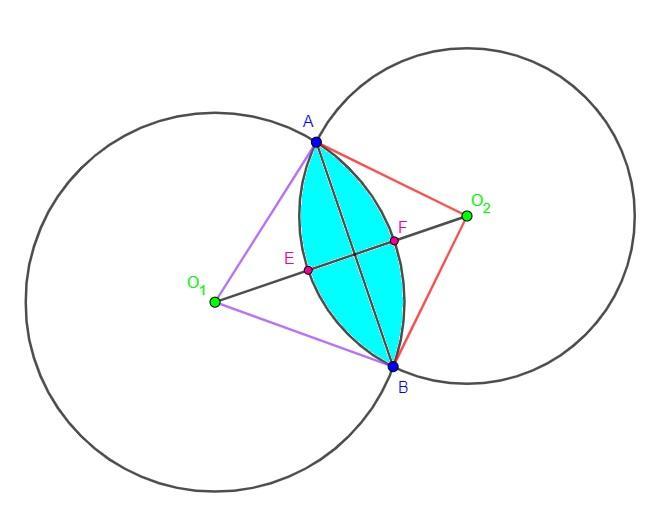
Дано: O₁,O₂ - центра окружностей, AO₁ = BO₁ = $\sqrt{3}$ см, AO₂ = BO₂ = 1 см, O₁O₂ = 2 см

Найти: S - ?

Решение:

По теореме косинусов для треугольника ΔAO₁O₂:

${AO_{2}}^{2} = {AO_{1}}^{2} + {O_{1}O_{2}}^{2} - 2 \cdot AO_{1} \cdot O_{1}O_{2} \cos \angle AO_{1}O_{2} \Longrightarrow$

$\Longrightarrow \angle AO_{1}O_{2} = \arccos\bigg ( \dfrac{ {AO_{1}}^{2} + {O_{1}O_{2}}^{2} - {AO_{2}}^{2}}{2 \cdot AO_{1} \cdot O_{1}O_{2} } \bigg ) =$

$= \arccos\bigg ( \dfrac{ (\sqrt{3} )^{2} +2^{2} - 1^{2}}{2 \cdot 2\cdot \sqrt{3} } \bigg ) = \arccos \bigg ( \dfrac{3 + 4 - 1}{4\sqrt{ 3} } \bigg ) = \arccos \bigg ( \dfrac{6}{4\sqrt{3} } \bigg ) = \arccos \bigg ( \dfrac{3}{2\sqrt{3} } \bigg ) =$

$= \arccos \bigg ( \dfrac{3\sqrt{3}}{2\sqrt{3} \cdot \sqrt{3} } \bigg ) = \arccos \bigg ( \dfrac{3\sqrt{3}}{2 \cdot 3} \bigg ) = \arccos \bigg ( \dfrac{\sqrt{3}}{2} \bigg ) = 30^{\circ}$.

${AO_{1}}^{2} = {AO_{2}}^{2} + {O_{1}O_{2}}^{2} - 2 \cdot AO_{2} \cdot O_{1}O_{2} \cos \angle AO_{2}O_{1} \Longrightarrow$

$\Longrightarrow \angle AO_{2}O_{1} = \arccos\bigg ( \dfrac{{AO_{2}}^{2} + {O_{1}O_{2}}^{2} - {AO_{1}}^{2}}{2 \cdot AO_{2} \cdot O_{1}O_{2} } \bigg ) =$

$= \arccos\bigg ( \dfrac{ 1^{2} +2^{2} - (\sqrt{3} )^{2}}{2 \cdot 1\cdot2} \bigg ) =\arccos\bigg ( \dfrac{1 +4 -3}{2 \cdot2} \bigg ) = \arccos\bigg ( \dfrac{2}{2 \cdot2} \bigg ) =$

$= \arccos\bigg ( \dfrac{1}{2} \bigg ) = 60^{\circ}$.

Треугольник ΔO₁AO₂ = ΔO₁BO₂ по третьему признаку равенства треугольников, так как AO₁ = BO₁, AO₂ = BO₂ - по условию, а сторона O₁O₂ - общая.

Так как треугольник ΔO₁AO₂ = ΔO₁BO₂, то по свойствам равных треугольников их соответствующие элементы равны, тогда угол ∠AO₁O₂ = ∠BO₁O₂ = 30°, ∠AO₂O₁ = ∠BO₂O₁ = 60°, следовательно:

∠AO₁B = ∠AO₁O₂ + ∠BO₁O₂ = 30° + 30° = 60°.

∠AO₂B = ∠AO₂O₁ + ∠BO₂O₁ = 60° + 60° = 120°.

По формуле площади сегмента, который отсекается хордой AB и дугой ∪AFB:

$S_{1} = \dfrac{{AO_{1}}^{2}}{2} \bigg ( \dfrac{\pi \angle AO_{1}B }{180^{\circ}} - \sin \angle AO_{1}B\bigg ) = \dfrac{(\sqrt{3} )^{2}}{2} \bigg ( \dfrac{60^{\circ}\pi }{180^{\circ}} - \sin 60^{\circ}\bigg )=$

$= \dfrac{3}{2} \bigg ( \dfrac{\pi }{3} - \dfrac{\sqrt{3} }{2} \bigg )= \dfrac{3\pi }{2 \cdot 3} - \dfrac{3\sqrt{3} }{4} = \dfrac{\pi}{2} - \dfrac{3\sqrt{3} }{4}$ см².

По формуле площади сегмента, который отсекается хордой AB и дугой ∪AEB:

$S_{2} = \dfrac{{AO_{2}}^{2}}{2} \bigg ( \dfrac{\pi \angle AO_{2}B }{180^{\circ}} - \sin \angle AO_{2}B\bigg ) = \dfrac{1^{2}}{2} \bigg ( \dfrac{120^{\circ}\pi }{180^{\circ}} - \sin 120^{\circ}\bigg )=$

$= \dfrac{1}{2} \bigg ( \dfrac{2\pi }{3} - \sin(180^{\circ} - 120^{\circ}) \bigg )= \dfrac{1}{2} \bigg ( \dfrac{2\pi }{3} - \sin 60^{\circ} \bigg )= \dfrac{1}{2} \bigg ( \dfrac{2\pi }{3} - \dfrac{\sqrt{3} }{2} \bigg )=$

$= \dfrac{2\pi }{2 \cdot 3} - \dfrac{\sqrt{3} }{2 \cdot 2} = \dfrac{\pi }{3} - \dfrac{\sqrt{3} }{4}$ см².

Площадь общей части двух кругов с центрами в точках O₁ и O₂:

$S = S_{1} + S_{2} = \dfrac{\pi}{2} - \dfrac{3\sqrt{3} }{4} + \dfrac{\pi }{3} - \dfrac{\sqrt{3} }{4} = \dfrac{3\pi +2\pi }{6} - \dfrac{4\sqrt{3} }{4} = \dfrac{5\pi }{6} - \sqrt{3}$ см².