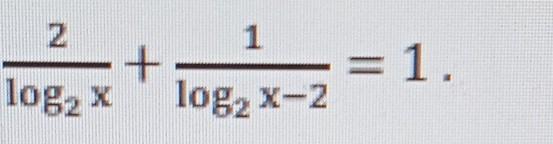Ответы
Ответ дал:
1
Ответ:
x₁ = 2 ; x₂ = 16
Пошаговое объяснение:
Найдём одз:
Пусть , таким образом:
Напишем над общим знаменателем:
Дробь равна нулю только когда числитель равен нулю:
Раскрываем скобки и вычисляем подобные:
Вернёмся к старой замене:
По одз корни подходят .
Ответ: x₁ = 2 ; x₂ = 16
Вас заинтересует
1 год назад
3 года назад
3 года назад
8 лет назад
8 лет назад