Помогите решить примеры на лимиты и производную, если можно то с пошаговым описанием действий
Приложения:
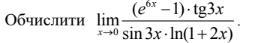
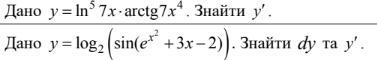
Ответы
Ответ дал:
1
Ответ:
Объяснение:
Вычислить предел:
Подставим 0:
Получили неопределенность 0/0.
Воспользуемся правилом Лопиталя. Найдем производную числителя и знаменателя:
Если мы подставим 0, то получим опять неопределенность 0/0.
Воспользуемся еще раз правилом Лопиталя.
Сначала найдем отдельно производную числителя:
Найдем производную знаменателя:
Запишем полученный предел:
1.
Вычислить производную:
2. Найти dy:
dy=y'dx
Формулы производных сложных функций см. в приложении.
#SPJ1
Приложения:

Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад