Угол А треугольника ABC в два раза больше угла В. Биссектриса угла 4 делит сторону ВС на отрезки ВК = 6 и КС = 3. Найдите стороны треугольника ABC.
Ответы
Ответ дал:
2
Ответ:
рассмотрим треугольник АКС и треугольник ABC так треугольник akc и треугольник abk ABC эти треугольники подобные так как треугольнике ABC угол А =2x а угол B = X и в треугольнике akc угол а = X угол K = 2x поэтому поэтому АБ / 6 = 9 / AC следовательно а б умножить на AC = 54. до этого на рисунке мы показали что AB = 2ac. теперь вместо AB поставим два АС то есть AB = 2ac получаем ac² = 27 и отсюда AC = 3√3. AB = 2 x 3 √3 2 х 2 = 6 √3 таким образом мы нашли все стороны треугольника.
Приложения:
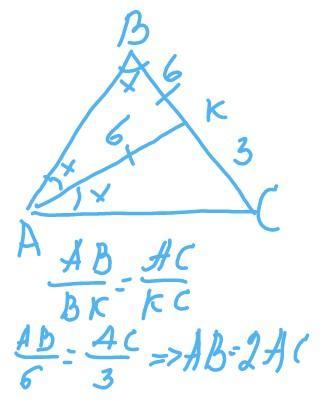
Аноним:
Здравствуйте. вы не могли бы мне помочь Завтра с геометрия пожалуйста умоляюю
Вас заинтересует
1 год назад
1 год назад
3 года назад
8 лет назад