Найти развязки системы уравнений:
На фото
Плизз дам 80 баллов
Приложения:
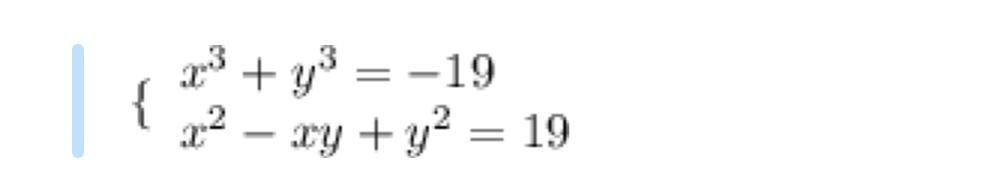
aarr04594:
Якщо перше рівняння розділити на друге, то отримаємо рівняння х+у=-1. Тоді якщо у=-х-1, то підстановкой у друге рівняння, отримаємо рівняння з однією невідомою.
х²-х(-х-1)+(-х-1)²=19,
х²+х²+х+х²+2х+1=19
3х²+3х-18=0, х²+х-6=0, х1=2, х2=-3, тоді у1=-3, у2=2. Відповідь: (2;-3), (-3; 2)
Ответы
Ответ дал:
0
Ответ:
Применяем формулу куба суммы : .
Вас заинтересует
1 год назад
3 года назад
3 года назад
8 лет назад
8 лет назад