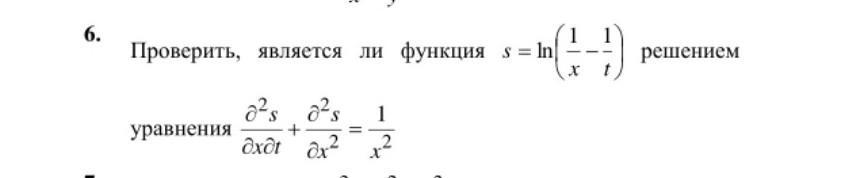Ответы
Ответ дал:
2
Ответ:
Проверим верность равенства. Найдём частные производные .
Подставим найденные производные в уравнение .
Равенство верно ⇒ заданная функция S(x,t) является решением
заданного дифференциального уравнения .
Приложения:

Alexxx0013:
к сожалению и это красный показывает
см скриншот
спасибо большое
см скрин
да посмотрел
если будет время еще помогите пожалуйста
можно и кнопочки нажать
какие ?
Ответ дал:
1
Ответ: является.
Объяснение:
Вас заинтересует
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад