Question

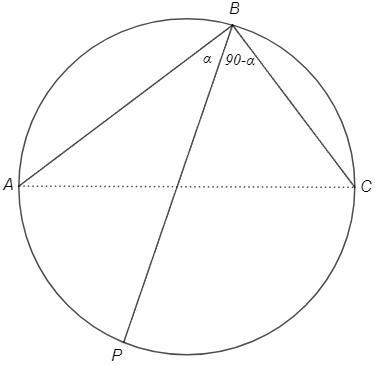
ΔABC - прямоугольный , вписанный в окружность ∠ABC = 90. Точка P на окружности такая , что B и P по разные стороны от стороны AC и

cos³∠ABP + cos³∠PBC = 91/125. Найти сумму всевозможных значений tg∠ABP

Answer 1

ABP =a ; PBC =90-a

cos³ABP + cos³PBC =cosa^3 +cos(90-a)^3

=sina^3 +cosa^3 =(sina+cosa)(sina^2 -sinacosa +cosa^2)

=(sina+cosa)(1 -sinacosa)

=√(1 +sin2a)(1 -sin2a/2) =91/125

Только два решения: a и 90-a

Найти: tga +tg(90-a) =tga +ctga =2/sin2a

t=√(1 +sin2a) => sin2a =t^2 -1

1<t<√3

t(3-t^2)/2 =91/125 => 125t^3 -125*3t +182 =0

Возможные делители числителя: 7, 13; в знаменателе 5

Угадываем: t=7/5

(5t -7)(25t^2 +35t -26)=0

Два других корня не проходят ОДЗ

sin2a=49/25 -1 =24/25

Ответ: 2/sin2a =25/12