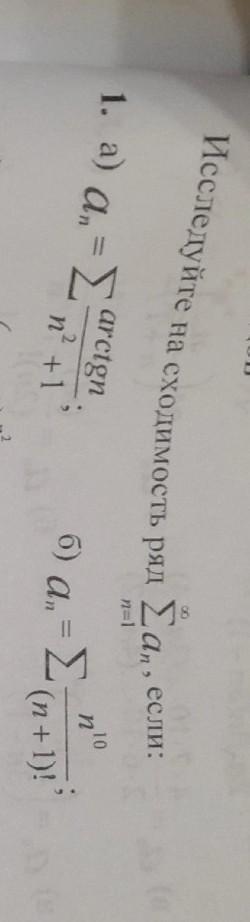Ответы
Ответ дал:
1
Ответ:
оба ряда сходятся.
Объяснение:
посмотрите предложенный вариант (вложение); оформление не соблюдалось.
Приложения:

veronikamila65:
спасибо большое
можете посмотреть 3 вопрос, мне решили , но там не все написано
могу тот ВОВ повторно добавить если вы попробуйте решить, пожалуйста)
вы сделали замену ?
вы здесь?
Ответ дал:
2
Ответ:
Исследовать числовые ряды на сходимость .
- знакоположительный числовой ряд .
Применяем достаточный интегральный признак сходимости Коши.
Составим функцию . Это положительная непрерывная и убывающая функция на
. Вычислим несобственный интеграл
Так как несобственный интеграл равен const , то он сходится , а вместе с ним сходится и заданный ряд .
- знакоположительный числовой ряд .
Применим к этому ряду достаточный признак сходимости Даламбера .
Вычислим предел отношения последующего члена ряда к предыдущему.
Так как предел равен числу, меньшему 1 , то ряд заданный сходится .
Приложения:


спасибо большое
посмотрите 3 мой вопрос который ответили пожалуйста, я там не могу понять как решили yugolovin решил
а неправильно
нужно сделать замену
всё правильно, замену делают в интеграле , чтобы было более понятно, чему равна первообразная . Это устный интеграл, зачем замену писать - лишние действия ...
понятно, хорошо
если решать с заменой, то t=arctgx , dt=dx/1+x^2 и интеграл будет от t*dt , что равно t^2/2 ... и ещё надо замену пределов интегрирования писать ... куча писанины ...
можете посмотреть пожалуйста, я пару задач добавила
Вас заинтересует
1 год назад
1 год назад
3 года назад
3 года назад