Основою піраміди є ромб із діагоналями 8 см і 5 см. Знайдіть об’єм піраміди, якщо її висота дорівнює 6 см
Ответы
Ответ дал:
0
Площа ромба може бути знайдена як добуток його діагоналей, поділений на 2:
S = (d1 * d2) / 2
де d1 та d2 - діагоналі ромба.
За теоремою Піфагора в прямокутному трикутнику з катетами 4 см і 2.5 см та гіпотенузою (довжина бічної грані піраміди) b, маємо:
b^2 = 4^2 + 2.5^2
b ≈ 4.69 см
Об'єм піраміди можна знайти як добуток площі основи та висоти, поділений на 3:
V = (S * h) / 3
де h - висота піраміди.
Підставляючи відомі значення, маємо:
S = (8 * 5) / 2 = 20 кв.см
V = (20 * 6) / 3 = 40 куб.см
Отже, об'єм піраміди дорівнює 40 кубічних сантиметрів.
S = (d1 * d2) / 2
де d1 та d2 - діагоналі ромба.
За теоремою Піфагора в прямокутному трикутнику з катетами 4 см і 2.5 см та гіпотенузою (довжина бічної грані піраміди) b, маємо:
b^2 = 4^2 + 2.5^2
b ≈ 4.69 см
Об'єм піраміди можна знайти як добуток площі основи та висоти, поділений на 3:
V = (S * h) / 3
де h - висота піраміди.
Підставляючи відомі значення, маємо:
S = (8 * 5) / 2 = 20 кв.см
V = (20 * 6) / 3 = 40 куб.см
Отже, об'єм піраміди дорівнює 40 кубічних сантиметрів.
Ответ дал:
0
начало на фото .V=1/3×20×6=40см³
Приложения:
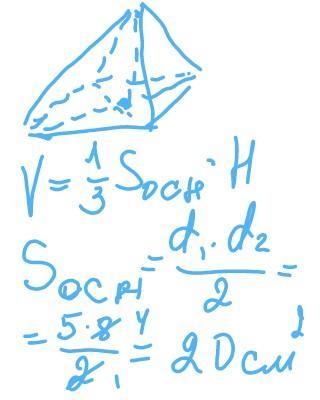
Вас заинтересует
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад