Question

Помогите, 100 баллов прошу вас

Найдите высоту равнобедренной трапеции , если ∠АСD = 90°, AD2 − BC2 = 64.

Answer 1

Ответ:

4 ед. изм.

Объяснение:

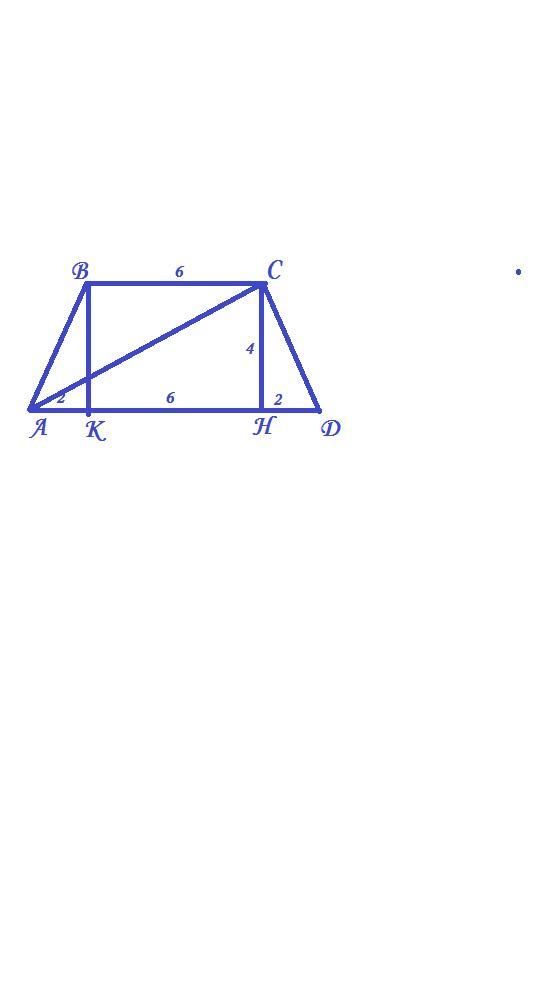
Дано: АВСД - трапеция, АВ=СД;  ∠АСD = 90°,  AD² − BC² = 64.  СН - ?

Проведем высоты ВК и СН.

AD² − BC² = 64, значит, (AD-ВС)(AD+ВС)=64.

64=4*16, отсюда AD-ВС=4,  AD+ВС=16.

Имеем систему уравнений, которую решаем способом сложения:

AD-ВС=4,  

AD+ВС=16

2AD=20;  AD=10;  ВС=16-10=6.

КН=ВС=6;   ΔАВК=ΔDСН по катету и гипотенузе, значит

АК=DН=(10-6):2=2.;  АН=2+6=8

ΔАСD - прямоугольный, значит

СН=√(АН*DН)=√(8*2)=√16=4 (ед. изм.)