Ответы
Ответ дал:
0
Ответ:
We can simplify the given equation using the trigonometric identity:
sin^2 x + cos^2 x = 1
First, we'll use the identity 6cos2x = 6(1 - sin^2 x) to substitute for cos2x:
6cos2x + 8sin^2 x - 5 = 0
6(1 - sin^2 x) + 8sin^2 x - 5 = 0
6 - 6sin^2 x + 8sin^2 x - 5 = 0
2sin^2 x + 1 = 0
Now, we'll isolate sin^2 x by moving the constant term to the other side:
2sin^2 x = -1
Dividing both sides by 2:
sin^2 x = -1/2
Since sin^2 x is always non-negative, there is no solution to this equation.
Therefore, the given equation 6cos2x+8sin^2 x-5=0 has no real solutions.
Объяснение:
Ответ дал:
0
Ответ:
все на фото аооалалалалалалккла
Приложения:
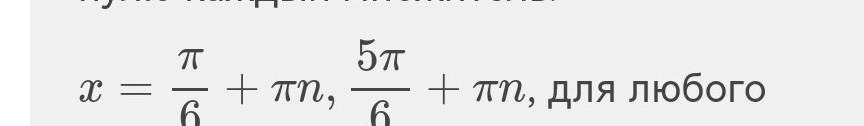
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
