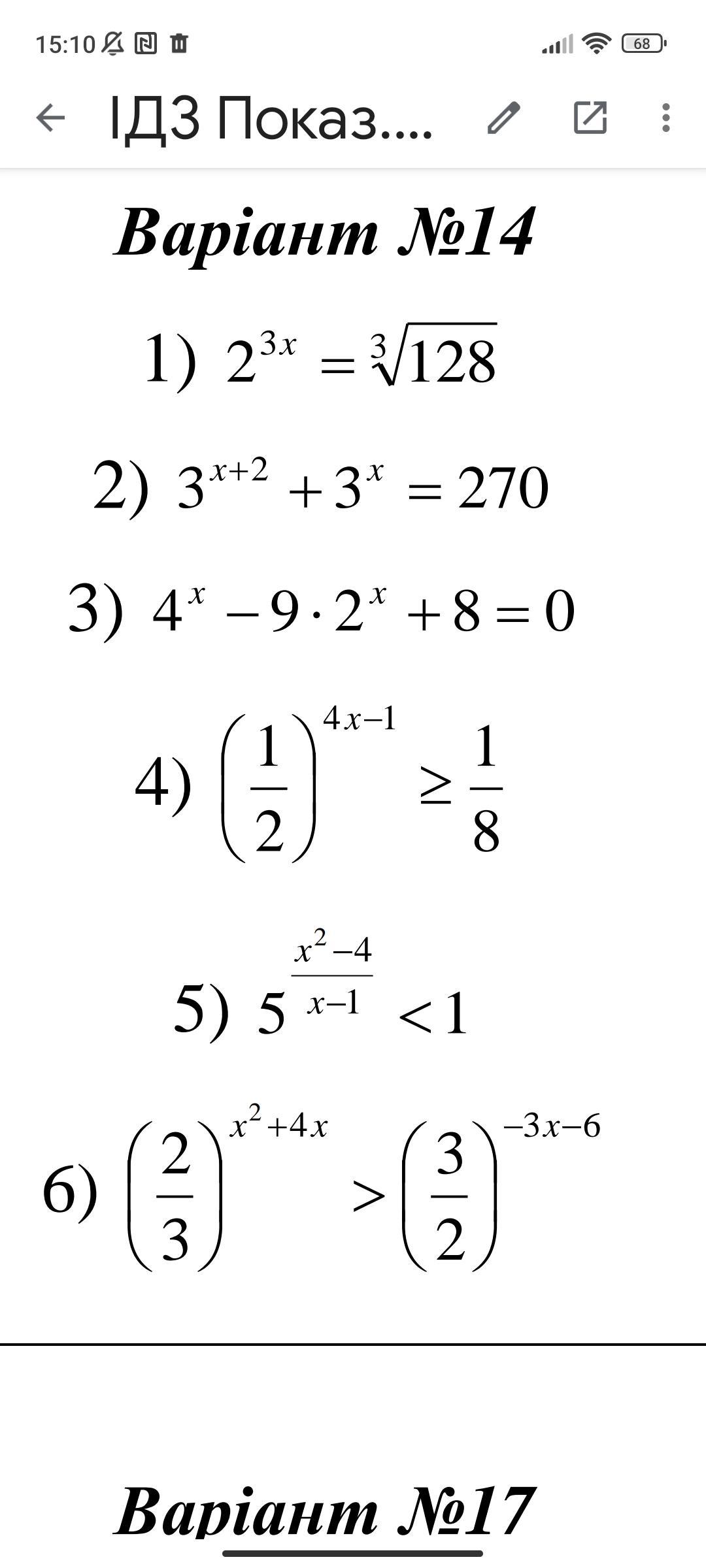Question

Задание на фото срочно

Answer 1

1) 2^(3x)  = 128 = 2^7,

3x = 7,

x = 7/3.

2) 3^(x + 2) + 3^x = 270 = 2·3^3·5,

(3^x)*3^2 + 3^x = 2·3^3·5 = 10*3^3,

(3^x)*(3^2 + 1) = 10*3^3,

(3^x)*(9 + 1) = 10*3^3,

(3^x)*10 = 10*3^3,

3^x = 3^3,

x = 3.

3) 4^x – 9*(2^x) + 8 = 0,

4^x = (2^2)^x = (2^x)^2.

Примем (2^x) = t.

t²  - 9t + 8 = 0,

D = 81 – 4*1*8 = 49, √D = +-7,

t1 = (9 – 7)/2 = 1,

t2 = (9 + 7)/2 = 8.

(2^x) = 1 = 2^0,

x1 = 0,

(2^x) = 8 = 2^3,

x2 = 3.

4) (1/2)^(4x – 1) >= (1/8) >= (1/2)^3,

4x – 1 >= 3,

4x >= 4.

x >= 4/4 >= 1.