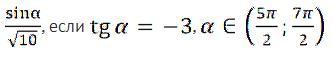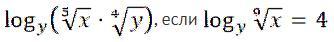Question

Решить задания на фото

Answer 1

Ответ:

1)  Так как   $\bf tga=-3$  , то   $\bf ctga=\dfrac{1}{tga}=-\dfrac{1}{3}$   .

Известно тождество   $\bf 1+ctg^2a=\dfrac{1}{sin^2a}$  .  Тогда

$\bf \dfrac{1}{sin^2a}=1+\dfrac{1}{9}=\dfrac{10}{9}\ \ \ \Rightarrow \ \ \ sin^2a=\dfrac{9}{10}\ \ ,\ \ \ sina=\pm \dfrac{3}{\sqrt{10}}$  

Если  $\bf a\in \Big(\ \dfrac{5\pi }{2}\ ;\ 3\pi \ \Big)$  ,  то   $\bf sina > 0$   и   $\bf sina=\dfrac{3}{\sqrt{10}}$  ,  тогда  

$\bf \dfrac{sina}{\sqrt{10}}=\dfrac{\dfrac{3}{\sqrt{10}}}{\sqrt{10}}=\dfrac{3}{10}=0,3$   .  

Если  $\bf a\in \Big(\ 3\pi \ ;\ \dfrac{7\pi }{2}\ \Big)$  ,  то   $\bf sina < 0$   и   $\bf sina=-\dfrac{3}{\sqrt{10}}$  ,  тогда  

$\bf \dfrac{sina}{\sqrt{10}}=\dfrac{-\dfrac{3}{\sqrt{10}}}{\sqrt{10}}=-\dfrac{3}{10}=-0,3$    .  

Учитывая, что  $\bf ctga=-\dfrac{1}{3} < 0$  , определяем , что угол может принад-

лежать интервалу  $\bf a\in \Big(\ \dfrac{5\pi }{2}\ ;\ 3\pi \ \Big)$   ,  поэтому запишем ответ.

Ответ:    $\bf \dfrac{sina}{\sqrt{10}}=0,3$   .

2)  Применим свойства логарифмов :

$\boldsymbol{log_{a}\, (x^{k})=k\cdot log_{a}\, x\ \ ,\ \ log_{a}(xy)=log_{a}\, x+log_{a}\, y}$  .

$\bf log_{y}\sqrt[9]{x}=4\ \ \ \Rightarrow \ \ \ \dfrac{1}{9}\, log_{y}\, x=4\ \ ,\ \ \ log_{y}\, x=36\ \ \ (\ x > 0\ ,\ y > 0\ ,\ y\ne 1\ )\\\\\\log_{y}(\sqrt[5]{x}\cdot \sqrt[4]{y})=\dfrac{1}{5}\, log_{y}\, x+\dfrac{1}{4}\, log_{y}\, y=\dfrac{1}{5}\cdot 36+\dfrac{1}{4}=\dfrac{149}{20}=7,45$