Ответы
Відповідь:
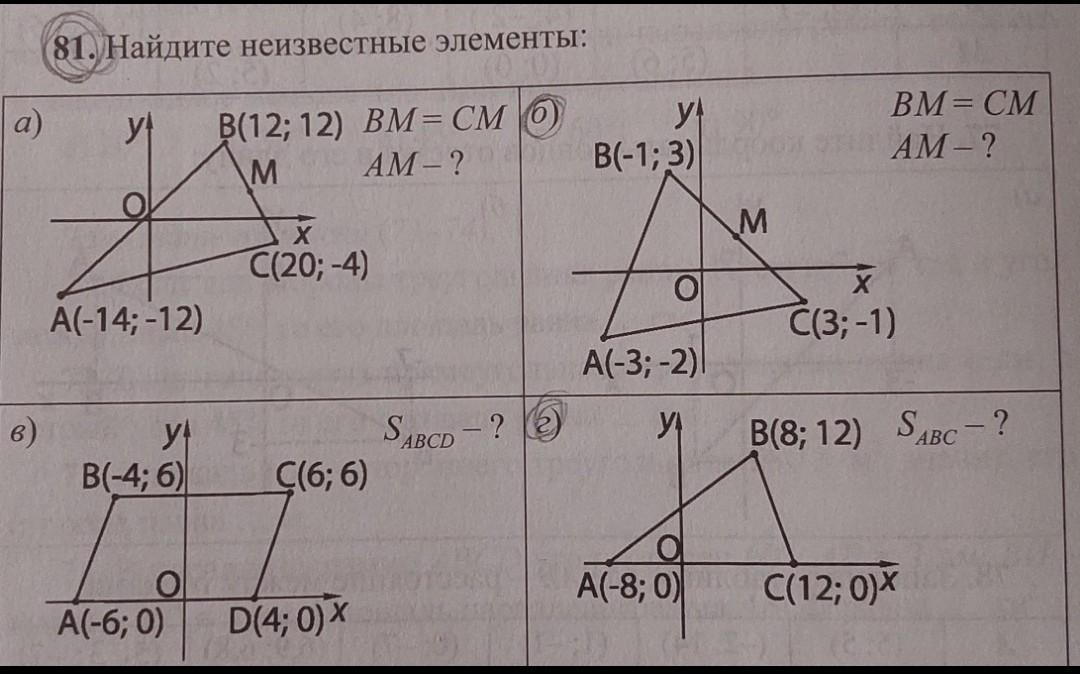
б) АМ = 5 единиц.
г) S∆авс = 120 единиц квадратных.
Покрокове пояснення:
б) Точка М - середина отрезка ВС, значит её координаты Х и У определяются как полусумма соответствующих координат точек В и С.
Хм = ( Хв + Хс ) / 2 = ( -1 + 3 ) / 2 = 2 / 2 = 1
Ум = ( Ув + Ус ) / 2 = ( 3 + ( -1 ) ) / 2 = 2 / 2 = 1
М ( 1, 1 )
Расстояние между двумя точками А и М на плоскости определяется по формуле:
L = √( ( Ха - Хм )² + ( Уа - Ум )² ) = √( ( -3 - 1 )² + ( -2 - 1 )² ) = √ ( 16 + 9 ) = √( 25 ) = 5 единиц
г) Площадь треугольника равна половине произведения длины основания на длину проведенной к этому основанию высоты.
В качестве основания возмем сторону АС - она лежит на оси ОХ и имеет нулевые координаты по оси ОУ, значит перпендикуляр проведенный на отрезок АС из точки В ( он перпендикулярен оси ОХ ) будет равен координате У точки В.
Высота треугольника H = 12 единицам.
Длина основания будет равна модулю разности координат Х точек А и С ( в общем случае используется формула для определения длины отрезка, которую мы применили в примере б; но здесь у нас координаты У точек А и С равны нулю, поэтому вместо того, чтобы возводить разницу координат Х в квадрат, а потом брать из неё корень квадратный ограничимся модулем; результат будет одинаковый ).
Lас = | -8 - 12 | = 20
S∆авс = 1/2 × Lас × H =1/2 × 20 × 12 = 120 единиц квадратных.