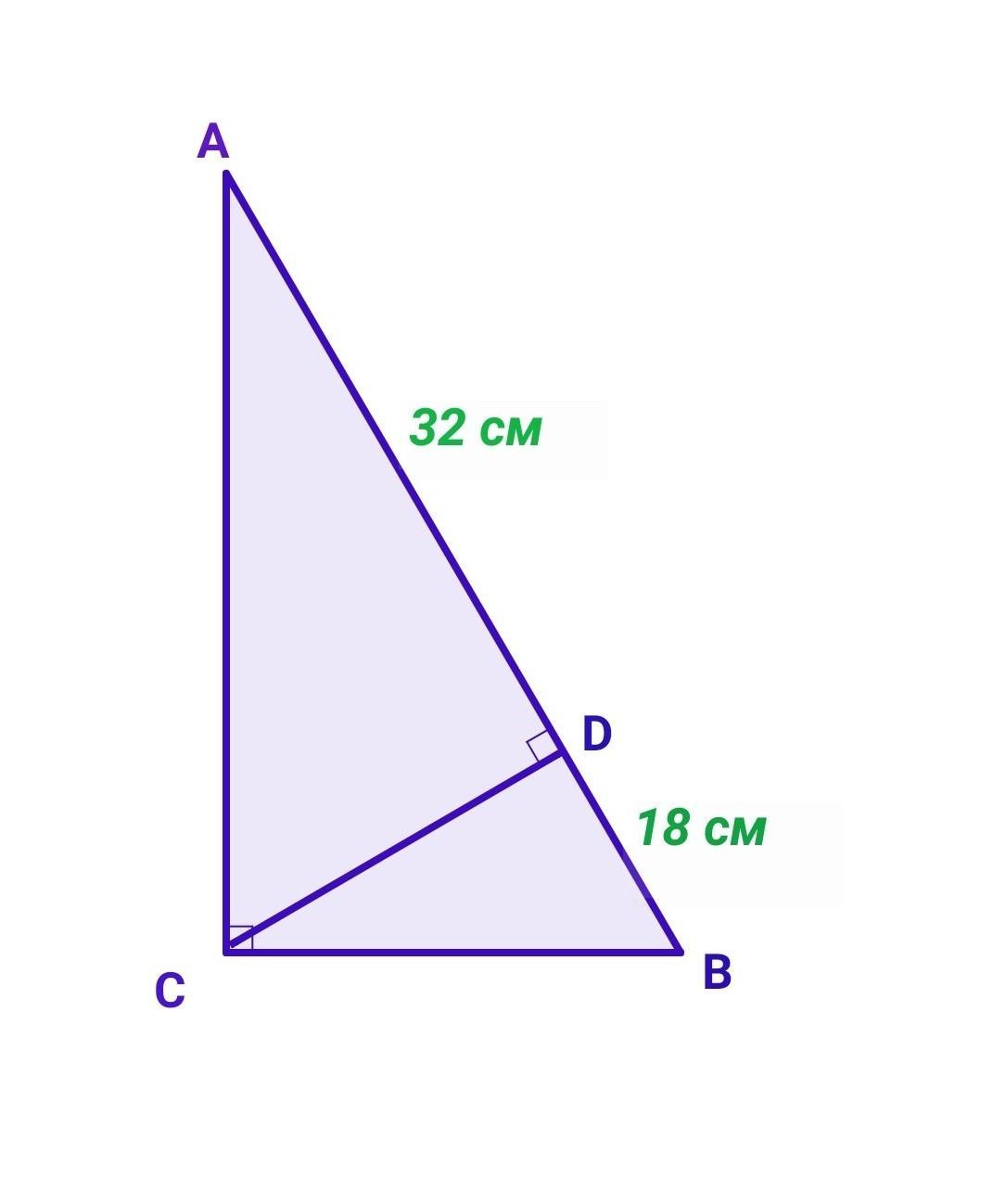
У прямокутному трикутнику знайдіть невідомі сторони, якщо проекції катетів на гіпотенузу дорівнюють 18 см і 32 см. Срочно !!!!!! Даю 50 балов
Ответы
Ответ:
30 см, 40 см, 50 см.
Объяснение:
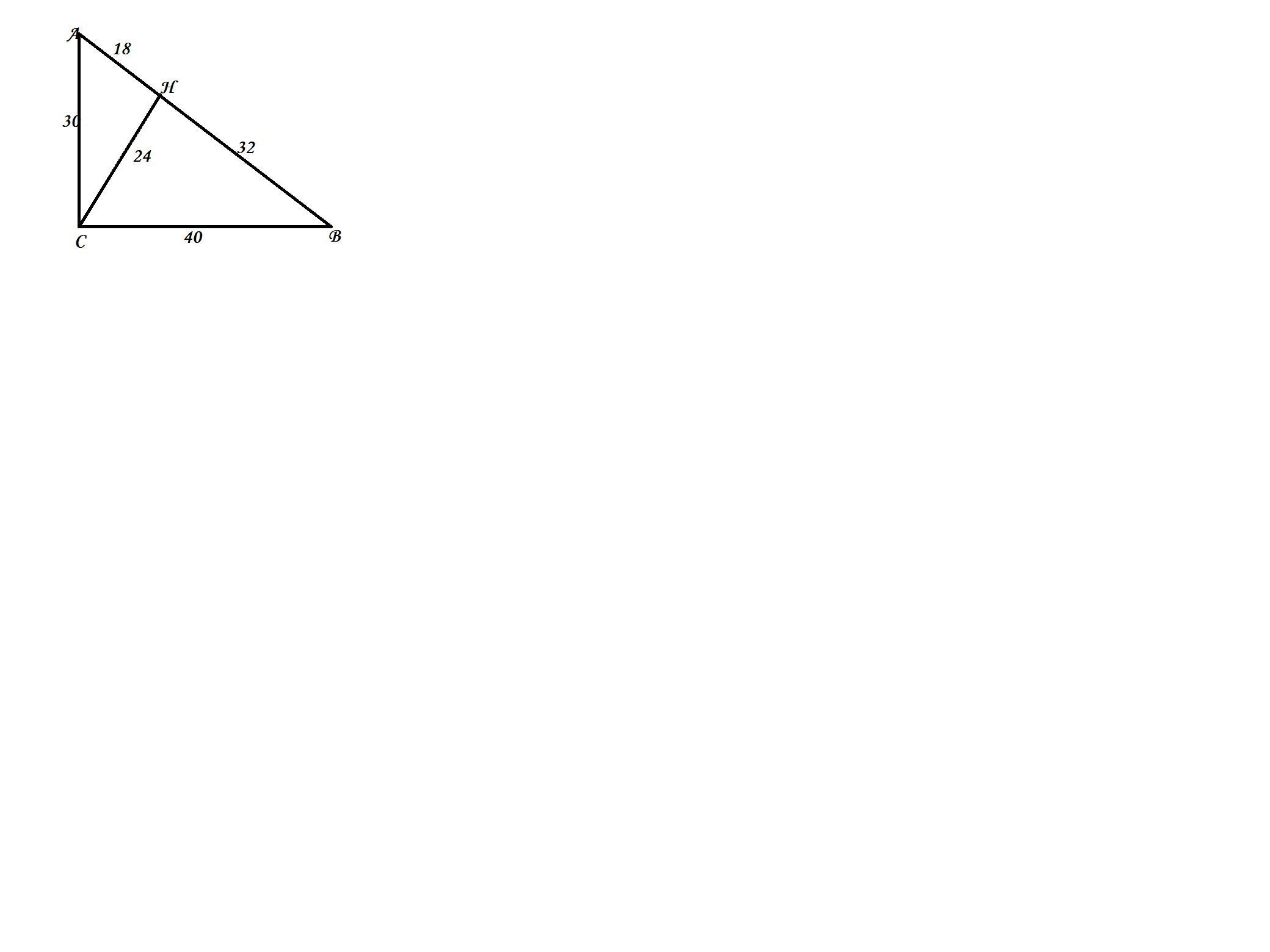
Дано: ΔАВС; ∠С=90°, СН - висота, АН=18 см, ВН=32 см.
АВ, ВС, АС - ?
АВ=18+32=50 см.
СН=√(АН*ВН)=√(18*32)=√576=24 см.
По теореме Пифагора АС=√(АН²+СН²)=√(576+324)=√900=30 см.
АС=30 см, АВ=50 см, значит ВС=40 см (египетский треугольник)
Ответ:
Катети прямокутного трикутника: 40 см, 30 см.
Гіпотенуза: 50 см
Объяснение:
У прямокутному трикутнику знайдіть невідомі сторони, якщо проекції катетів на гіпотенузу дорівнюють 18 см і 32 см.
Нехай дано △АВС - прямокутний, ∠С=90°. CD⟂AB. AD=32 см, BD=18 см.
1) За аксиомою вимірювання відрізків отримаємо:
AB=AD+BD=32+18=50 (см).
За метричними співвідношеннями у прямокутному трикутнику маємо:
2) CD²=AD•BD
3) AC²=AB•AD
4) BC²=AB•BD
Відповідь: 30 см, 40 см, 50 см