Question

30 Балів!!! Будь-ласка допоможіть якнайшвидше!!!

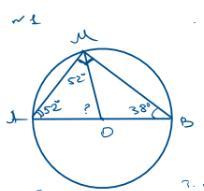
1. У колі з центром O проведено діаметр AB та хорди AM і MB. Знайти кути △ AMB, якщо ∠ AOM = 78° (рис. 1).
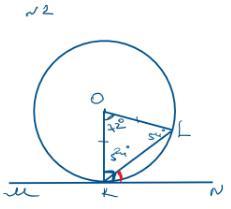
2. Пряма MN дотикається до кола із центром у точці O (K- точка дотику). Знайти ∠LOK, якщо ∠NKL = 34° (рис. 2).

Answer 1

Ответ:

вот решение

Объяснение:

на листочке

Answer 2

Відповідь:

No1

Дано: коло з центром О, Ав - діаметр, Ам і МВ - хорди, кут АОМ = 78.

Знайти: кут А, кут М, кут В.

Розв‘язання:

трикутник АОМ - рівнобедрений (ОА=ОМ=R), звідси маємо, що кут ОАМ = кут ОМА = (180-78)*1\2 = 51.

трикутник МОВ - рівнобедрений (ОМ=ОВ=R), тому за властивістю зовнішнього кута, кут ОВМ = кут ОМВ = 78*1/2 = 39.

кут АМВ = 51 + 39 = 90.

Відповідь: 51, 90, 39.

No2

Дано: коло з центром О, МN - дотична, К - точка дотику, кут NКL = 34.

Знайти: кут LOK.

Розв‘язання:

ОК перпендикулярний МN за властивістю дотичної.

кут ОКL = 90 - 34 = 56.

трикутник KOL - рівнобедрений (OK=OL=R), звідси маємо, що кут LOK = 180 - 56*2 = 68.

Відповідь: 68.

Пояснення:

Всі пояснення є у відповіді. Малюнок і умова не збігаються, тому робила за текстовою інформацією.