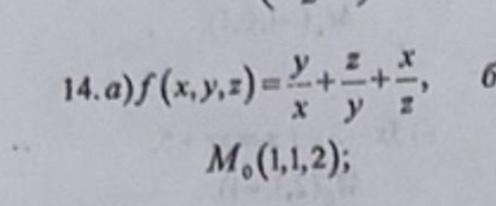Ответы
Ответ дал:
0
Ответ:
Частные производные 1 порядка .
При нахождении производной по одной из переменных другие переменные считаются константами .
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
8 лет назад